Функциональный метод: Функциональный анализ

Функциональный анализ

Содержит изложение первоначальных основ функционального анализа и тех его направлений, которые непосредственно примыкают к прикладным задачам. Изложены: метод малого параметра, метод продолжения по параметру, приближенные (в частности, разностные) методы решения уравнений, метод Галеркина и метод конечных элементов (приближение сплайнами), элементы выпуклого анализа, метод монотонных операторов и другие вопросы. Второе издание — 1993 г. Для студентов вузов, обучающихся по специальностям > и >, для преподавателей и лиц, интересующихся приложениями функционального анализа.

Автор	Треногин Владилен Александрович
Издательство	ООО «Физматлит»
Дата издания	2002
Кол-во страниц	488
ISBN	978-5-9221-0272-8
Тематика	Математика. Прикладная математика
№ в каталоге	272

Категории: Учебная литература

краткое описание, особенности применения и примеры

Процесс познания в теоретических науках осуществляется посредством специальных методов. В отличие от практики, здесь исследование ведется через мысленный анализ сторон объекта. Структурно-функциональный метод подразумевает четкое обозначение границ изучаемого явления. Науки, в которых наиболее часто он используется: история, культурология, книговедческие и политологические, а также юриспруденция и криминология. Зачастую он является основным и определяющим в исследовании. Поэтому этому типу анализа уделяется столь большое значение.

О методологии наук

На теоретическом уровне познания используют не только универсальные методы, но и специальные. К первым относят те, что подходят для любого случая: анализ, моделирование, формализация. Среди частнонаучных выделяют следующие методы познания: исторический, системный, структурный, функциональный. В отдельных случаях их называют подходами. Они могут пересекаться в разных областях знания или быть дополнены еще более узкоспециальными (например, библиографический метод в книговедении). Системный подход иногда подразумевает анализ структуры и функций предмета, исторический же стоит в некотором обособлении. Но использование их всех в теории значительно обогащает научную сферу.

Описание

Метод включает две составляющие. Структура подразумевает строение какого-либо объекта, деление его на элементы. Некоторые из них являются главенствующими, есть и совсем незначительные. Но характерная черта – их связь друг с другом. Каждый пункт имеет свое определенное место в системе. Другая составляющая структурно-функционального метода исследования связана с ролью и предназначением этих элементов. Выносится на рассмотрение их характеристика и выполняемые в соответствии с ней функции. А, соответственно, и влияние элементов на объект в целом и внешнюю среду.

Оба компонента тесно переплетаются в функционально-структурном методе, позволяя ему более полно охарактеризовать стороны явления. Близким к понятию структуры является термин «система». Потому в некоторых случаях под одним названием объединяют два метода: структурно-функциональный и системный. Однако для некоторых наук их принято разграничивать.

Особенности применения

Чисто структурный метод используют в более широком спектре наук и дисциплин. Он незаменим для лингвистики, литературоведения и даже для естественных наук (физики, биологии). Применяется для подробного анализа произведений искусства и некоторых языковых единиц. Особое внимание уделяется исследованию связей. Каждая часть оказывает воздействие на другую, и в результате – на всю систему. В этом состоит одно из проявлений функций элементов. В итоге удается прослеживать развитие и постепенное преобразование предмета и окружающей действительности.

Используют метод в журналистике в тесном переплетении с историей, обращая внимание на исторические факты, предшествующие появлению объекта. Масс-медиа выполняют множество функций, воздействуя на общество в целом. Например, передают и интерпретируют информацию, развлекают и комментируют важные события. Структурно-функциональный метод в журналистских изысканиях содействует формированию терминологии и классификации науки. В современном мире роль коммуникаций изучается для совершенствования их влияния на человечество.

Специфика метода в культурологии

Неопределенность границ предмета исследования затрудняет применение структурно-функционального метода в культурологии. Понятия этой науки абстрактны и не связаны с материей. Потому анализ конкретных явлений в данной науке имеет свои особенности.

К примеру, если изучается способ поведения личности, то берется за основу некий эталон, с которым он сравнивается. Действия человека оцениваются в конкретно заданной ситуации и в определенном окружении. Выбирается даже некий отрезок времени. Только после этого можно выявить структуру предмета исследования и провести ее анализ. Ограничения в данном случае необходимы.

В философии и социологии

На Западе метод появился в начале прошлого века. С его помощью изучали общество и действующие в нем процессы. Известные социологи из Америки и Европы занимались этой проблемой. В их числе американец Т. Парсонс, особое внимание акцентирующий на действиях людей. Он считал их основным объектом изучения, чтобы в полной мере понять закономерность, существовавшую в обществе.

Впоследствии многие ученые подвергали критике подобные взгляды и вносили новшества в анализ. Структурно функциональный метод в социологии совершенствовался и развивался. С его помощью изучали отклонения, свойственные и несвойственные общественным процессам. В конце прошлого века на непродолжительный период о нем практически забыли, сейчас же – заново возрождается и активно используется в науке. Изучается уже не только общество в целом, но и группы людей, институты, различные объединения.

В истории и политологии

Большинство методов в исторической науке берут за основу исторический подход и вытекают из него. Появляются особые сочетания: историко-системный, историко-сравнительный и другие. Изучаются предпосылки явлений и в то же время делаются попытки предсказать будущее, предположить дальнейшее развитие событий. В этом помогает и структурно-функциональный метод. Объект исследования разбивается на структурные части, и все внимание приковывается к значению каждой из них в ту или иную эпоху (отрезок времени).

В политологии подобный способ считается относительно современным: его начали применять лишь с середины прошлого века. Основной задачей стало выяснить, как правильно регулировать существование политического института и через него воздействовать на социум. Одним из первых исследователей в этой области был Д. Истон. Он выявил функции политической системы распределения ценностей между людьми и убеждение их в обязательности этого действия. Другой ученый Г. Алмонд больше внимания обращал на структуру и целесообразность тех или иных действий в политике. Политическую систему в целом он рассматривал через устремления отдельных личностей и групп, партий.

В экономике

Исходя из того, что все общественные сферы тесно взаимосвязаны, в изучении их влияния используются схожие подходы. Каждая представляет собой систему, состоящую из отдельных ячеек. Государство и политические структуры активно влияют на экономику. Ее элементы, в свою очередь, тесно взаимосвязаны с общественной сферой, благополучием населения, социумом.

В экономику метод структурно-функционального анализа пришел из социологических наук. Эта область зависит от множества факторов внешней среды. Уровень жизни населения, политическая нестабильность, законодательство в области предпринимательства могут привести к серьезным изменениям в экономике. Потому необходимо рассматривать ее функции в аспекте их связей с другими.

В криминологии и расследованиях

Преимущественно метод применяется в теоретических науках, но в некоторых случаях имеет значение и на практике. Некоторые его идеи прослеживаются в современных криминологических теориях. Специалистами тщательно изучались личности преступников, факторы, влияющие на рост убийств и преступлений. В рамках подхода пришли к выводу, что для спокойной жизни в обществе необходимо не только наличие социальных образований, но и убежденность населения в их действенности, работе, направленной на организацию порядка. Кражи и прочие негативные явления возрастают в периоды революций, нестабильной обстановки в стране.

Один из социологов, Э. Дюркгейм, предполагал, что преступность тоже выполняет некоторые функции. Она уравновешивает общественные процессы и содействует прогрессу. Но в обществе должен поддерживаться определенный уровень преступности. Чрезмерные ее проявления приведут к распаду государства.

Человек совершает противоправные поступки не только по причине своих склонностей, но и под воздействием внешних факторов. Это может быть и поведение группы, к которой принадлежит субъект, наличие у людей общих целей и способов их достижения. Устремления могут быть направлены на нечто положительное, средства же не всегда оказываются в рамках закона. Государственная система наказания является другим фактором, функции ее также следует подробно изучать.

В литературоведении

В изучении произведений искусства и процессов, происходящих в литературе, используются различные специфические подходы. Исследования проводятся по биографиям авторов, через явления эпохи создания романа (повести, цикла стихотворений), понимание его смысла и выявления системы используемых знаков. Последователи структурно-функционального метода рассматривают текст через художественные приемы. Писатель на основе имеющегося у него опыта и знаний особенностей строения произведения создает новый объект искусства. Эта вещь изначально предназначена конкретной группе читателей. Исследователи выявляют из текста схожие элементы, производят сравнительный анализ. Каждый прием имеет цель так или иначе воздействовать на публику, вызвать у нее положительные или отрицательные эмоции. В итоге прослеживается четкая цепь следования произведения от писателя к читателям.

Издания | Библиотечно-издательский комплекс СФУ

Все года изданияТекущий годПоследние 2 годаПоследние 5 летПоследние 10 лет

Все виды изданийУчебная литератураНаучная литератураЖурналыМатериалы конференций

Все темыЕстественные и точные наукиАстрономияБиологияГеографияГеодезия. КартографияГеологияГеофизикаИнформатикаКибернетикаМатематикаМеханикаОхрана окружающей среды. Экология человекаФизикаХимияТехнические и прикладные науки, отрасли производстваАвтоматика. Вычислительная техникаБиотехнологияВодное хозяйствоГорное делоЖилищно-коммунальное хозяйство. Домоводство. Бытовое обслуживаниеКосмические исследованияЛегкая промышленностьЛесная и деревообрабатывающая промышленностьМашиностроениеМедицина и здравоохранениеМеталлургияМетрологияОхрана трудаПатентное дело. Изобретательство. РационализаторствоПищевая промышленностьПолиграфия. Репрография. ФотокинотехникаПриборостроениеПрочие отрасли экономикиРыбное хозяйство. АквакультураСвязьСельское и лесное хозяйствоСтандартизацияСтатистикаСтроительство. АрхитектураТранспортХимическая технология. Химическая промышленностьЭлектроника. РадиотехникаЭлектротехникаЭнергетикаЯдерная техникаОбщественные и гуманитарные наукиВнешняя торговляВнутренняя торговля. Туристско-экскурсионное обслуживаниеВоенное делоГосударство и право. Юридические наукиДемографияИскусство. ИскусствоведениеИстория. Исторические наукиКомплексное изучение отдельных стран и регионовКультура. КультурологияЛитература. Литературоведение. Устное народное творчествоМассовая коммуникация. Журналистика. Средства массовой информацииНародное образование. ПедагогикаНауковедениеОрганизация и управлениеПолитика и политические наукиПсихологияРелигия. АтеизмСоциологияФизическая культура и спортФилософияЭкономика и экономические наукиЯзыкознаниеХудожественная литература

Все институтыВоенно-инженерный институтБазовая кафедра специальных радиотехнических системВоенная кафедраУчебно-военный центрГуманитарный институтКафедра ИТ в креативных и культурных индустрияхКафедра истории России, мировых и региональных цивилизацийКафедра культурологии и искусствоведенияКафедра рекламы и социально-культурной деятельностиКафедра философииЖелезногорский филиал СФУИнженерно-строительный институтКафедра автомобильных дорог и городских сооруженийКафедра инженерных систем, зданий и сооруженийКафедра проектирования зданий и экспертизы недвижимостиКафедра строительных конструкций и управляемых системКафедра строительных материалов и технологий строительстваИнститут архитектуры и дизайнаКафедра архитектурного проектированияКафедра градостроительстваКафедра дизайнаКафедра дизайна архитектурной средыКафедра изобразительного искусства и компьютерной графикиИнститут горного дела, геологии и геотехнологийКафедра геологии месторождений и методики разведкиКафедра геологии, минералогии и петрографииКафедра горных машин и комплексовКафедра инженерной графикиКафедра маркшейдерского делаКафедра открытых горных работКафедра подземной разработки месторожденийКафедра технической механикиКафедра технологии и техники разведкиКафедра шахтного и подземного строительстваКафедра электрификации горно-металлургического производстваИнститут инженерной физики и радиоэлектроникиБазовая кафедра «Радиоэлектронная техника информационных систем»Базовая кафедра инфокоммуникацийБазовая кафедра физики конденсированного состояния веществаБазовая кафедра фотоники и лазерных технологийКафедра нанофазных материалов и нанотехнологийКафедра общей физикиКафедра приборостроения и наноэлектроникиКафедра радиотехникиКафедра радиоэлектронных системКафедра современного естествознанияКафедра теоретической физики и волновых явленийКафедра теплофизикиКафедра экспериментальной физики и инновационных технологийКафедры физикиИнститут космических и информационных технологийБазовая кафедра «Интеллектуальные системы управления»Базовая кафедра геоинформационных системКафедра высокопроизводительных вычисленийКафедра вычислительной техникиКафедра информатикиКафедра информационных системКафедра прикладной математики и компьютерной безопасностиКафедра разговорного иностранного языкаКафедра систем автоматики, автоматизированного управления и проектированияКафедра систем искусственного интеллектаИнститут математики и фундаментальной информатикиБазовая кафедра вычислительных и информационных технологийБазовая кафедра математического моделирования и процессов управленияКафедра алгебры и математической логикиКафедра высшей и прикладной математикиКафедра математического анализа и дифференциальных уравненийКафедра математического обеспечения дискретных устройств и системКафедры высшей математики №2афедра теории функцийИнститут нефти и газаБазовая кафедра пожарной и промышленной безопасностиБазовая кафедра химии и технологии природных энергоносителей и углеродных материаловКафедра авиационных горюче-смазочных материаловКафедра бурения нефтяных и газовых скважинКафедра геологии нефти и газаКафедра геофизикиКафедра машин и оборудования нефтяных и газовых промысловКафедра разработки и эксплуатации нефтяных и газовых месторожденийКафедра технологических машин и оборудования нефтегазового комплексаКафедра топливообеспеченя и горюче-смазочных материаловИнститут педагогики, психологии и социологииКафедра информационных технологий обучения и непрерывного образованияКафедра общей и социальной педагогикиКафедра психологии развития и консультированияКафедра современных образовательных технологийКафедра социологииИнститут торговли и сферы услугБазовая кафедра таможенного делаКафедра бухгалтерского учета, анализа и аудитаКафедра гостиничного делаКафедра математических методов и информационных технологий в торговле и сфере услугКафедра технологии и организации общественного питанияКафедра товароведения и экспертизы товаровКафедра торгового дела и маркетингаОтделение среднего профессионального образования (ОСПО)Институт управления бизнес-процессамиКафедра бизнес-информатики и моделирования бизнес-процессовКафедра маркетинга и международного администрированияКафедра менеджмент производственных и социальных технологийКафедра цифровых технологий управленияКафедра экономики и управления бизнес-процессамиКафедра экономической и финансовой безопасностиИнститут физ. культуры, спорта и туризмаКафедра медико-биологических основ физической культуры и оздоровительных технологийКафедра теоретических основ и менеджмента физической культуры и туризмаКафедра теории и методики спортивных дисциплинКафедра физической культурыИнститут филологии и языковой коммуникацииКафедра восточных языковКафедра журналистики и литературоведенияКафедра иностранных языков для гуманитарных направленийКафедра иностранных языков для естественнонаучных направленийКафедра иностранных языков для инженерных направленийКафедра романских языков и прикладной лингвистикиКафедра русского языка и речевой коммуникацииКафедра русского языка как иностранногоКафедра теории германских языков и межкультурной коммуникацииИнститут фундаментальной биологии и биотехнологииБазовая кафедра «Медико-биологические системы и комплексы»Базовая кафедра биотехнологииКафедра биофизикиКафедра водных и наземных экосистемКафедра геномики и биоинформатикиКафедра медицинской биологииИнститут цветных металлов и материаловеденияБазовая кафедра «Технологии золотосодержащих руд»Кафедра автоматизации производственных процессов в металлургииКафедра аналитической и органической химииКафедра инженерного бакалавриата СDIOКафедра композиционных материалов и физико-химии металлургических процессовКафедра литейного производстваКафедра металловедения и термической обработки металловКафедра металлургии цветных металловКафедра обогащения полезных ископаемыхКафедра обработки металлов давлениемКафедра общаей металлургииКафедра техносферной безопасности горного и металлургического производстваКафедра физической и неорганической химииКафедра фундаментального естественнонаучного образованияИнститут экологии и географииКафедра географииКафедра охотничьего ресурсоведения и заповедного делаКафедра экологии и природопользованияИнститут экономики, государственного управления и финансовКафедра бухгалтерского учета и статистикиКафедра международной и управленческой экономикиКафедра социально-экономического планированияКафедра теоретической экономикиКафедра управления человеческими ресурсамиКафедра финансов и управления рискамиКрасноярская государственная архитектурно-строительная академияКрасноярский государственный технический университетКрасноярский государственный университетМежинститутские базовые кафедрыМежинститутская базовая кафедра «Прикладная физика и космические технологии»Политехнический институтБазовая кафедра высшей школы автомобильного сервисаКафедра конструкторско-технологического обеспечения машиностроительных производствКафедра материаловедения и технологии обработки материаловКафедра машиностроенияКафедра прикладной механикиКафедра робототехники и технической кибернетикиКафедра стандартизации, метрологии и управления качествомКафедра тепловых электрических станцийКафедра теплотехники и гидрогазодинамикиКафедра техногенных и экологических рисков в техносфереКафедра техносферной и экологической безопасностиКафедра транспортаКафедра транспортных и технологических машинКафедра химииКафедра электроэнергетикиХакасский технический иститутЮридический институтКафедра гражданского праваКафедра иностранного права и сравнительного правоведенияКафедра конституционного, административного и муниципального праваКафедра международного праваКафедра предпринимательского, конкурентного и финансового праваКафедра теории и истории государства и праваКафедра теории и методики социальной работыКафедра трудового и экологического праваКафедра уголовного праваКафедра уголовного процеса и криминалистики

По релевантностиСначала новыеСначала старыеПо дате поступленияПо названиюПо автору

Архив: Функциональный метод и форма.

1926

 

 

Гинзбург М. Я. Функциональный метод и форма // Современная архитектура. 1926. № 4. — С. 89—92.

 

ФУНКЦИОНАЛЬНЫЙ МЕТОД И ФОРМА

DIE FUNCTIONELLE МЕTHODE UND DIE FORM

 

 

Основной причиной, застававшей современного архитектора решительно порвать со старыми архитектурными приемами и канонами и заменить их методом функционального мышления, является коренное изменение нашей жизни: с одной стороны, ошеломляюще быстрое развитие техники, в котором, конечно, более всего повинны Западная Европа и Америка, развитие, которое сделало разницу в методах строительства нескольких десятилетий более ощутительной, чем разницу долгих веков исторического периода, с другой — не менее важное и коренное социальное изменение нашей жизни, касающееся более всего СССР, — два явления, которые и каждое порознь и оба вместе видоизменяют всю нашу хозяйственную и культурную жизнь.

 

Но диалектическое развитие жизни таково, что никогда не уничтожается одним взмахом старое и никогда но сооружается мгновенно новое.

Старое уже умерло — и вместе с тем еще по инерции продолжает существовать. Новое появилось, но еще не завоевало всех областей жизни. Трудящиеся СССР твердо стали па пути новой жизни, но еще миллионы крестьян и рабочих продолжают жить по-старине.

 

Точно так же, мировая техника непрерывно двигается вперед, но еще в очень многих областях, в особенности у нас, строительство продолжает ползти по самым из битым шаблонам, по проторенным порогам.

 

Новые вехи твердо устанавливаются наиболее прогрессивными жизненными факторами, нить новой жизни натягивается по ним, но за этими вехами самая разнообразная неразбериха, множество участков косности, рутины, участков отступления.

 

Метод функционального мышления прежде всего должен исходить из правильного учета этого диалектического развития жизни и всегда иметь своими предпосылками не участки отступления, а вехи новой жизни.

 

Только тогда он получает свой актуальный смысл. Пусть в каком-нибудь отдельном случае предпосылки еще старые — это участок отступления — правильно понятый функциональный метод мышления заставляет архитектора не делать непосредственных выводов из этих атавистических предпосылок, а через голову их отвечать тем новым вехам, которые установлены впереди.

 

Таким образом правильно понимаемый функциональный метод требует от современного архитектора, во всех без исключения случаях, материального оформления, вызываемого новыми условиями жизни.

 

Если в конечном счете у архитектора в результате его работы получилась форма атавистическая — значит функциональный метод применен неправильно, и решение в чем-то ложно. В данном случае полученное формальное решение может и должно служить проверкой правильности применения функционального метода, в такой же мере, как этот последний должен гарантировать архитектора от привнесения в его формальное решение лишних прибавочных, отвлеченно-эстетических элементов.

 

Великолепным примером, поясняющим нашу мысль, может служить рабочее строительство МОССОВЕТА.

 

Не нужно быть особо тонким ценителем архитектуры для того, чтобы при первом же взгляде, брошенном на внешность этих домов, убедиться не только в их атавистическом облике, но и вообще в полном отсутствии в них какой бы то ни было архитектурной мысли. И сейчас же эта формальная проверка подтверждает свою правильность. Рассмотрение этих домов с плановой стороны с очевидностью говорит нам, что перед нами участки отступления, что архитектора Моссовета шли не по вехам новой жизни. Действительно, рабочие дома Моссовета самые обыкновенные „доходные дома“ с уменьшенной жилой площадью, никакого нового социального элемента здесь не усмотрено. От того, что в них живут рабочие, „социальное“ качество их архитектуры не изменилось, — никаких новых социальных функций здесь нет, и обитатели этого дома, конечно, не смогут в них сделать какого-либо даже самого ничтожного шага в оформлении нового быта.

 

С другой стороны, примененные в этих домах конструкции, употребленные материалы также не сдвигают с мертвой точки вопросов новой архитектуры. И эта область в домах Моссовета атавистична насквозь.

 

Таким образом ясно, что архитектурная форма нас здесь не обманула. Атавизм оформления — функция атавистического подхода по существу. Характерно, что Моссовет, очевидно, сознавал неудовлетворительность архитектуры этих домов, объявляя в свое время конкурс на украшение фасадов.

 

Но в том и дело, что сама идея „украшения“ фасада хотя бы в самом новом, что ни на есть стиле, есть идея ложная и не современная, так как, действительно, современная архитектура, архитектура, выражающая нашу новую эпоху, — не требует никакого „фасада». Эта архитектура естественно и неизбежно получается, как функция правильно понятых новых производственно-бытовых взаимоотношений, новых строительных материалов и методов их употребления.

 

Непосредственно ответить на все поставленные вопросы экономического и конструктивного характера, давая при этом атавистические решения, а это в сложном переплетении современности, как мы видим, возможно, значит, кроме того, еще не доучесть целый ряд предпосылок, предпосылок более сложного характера, всегда вытекающих из функционального назначения вещей, но не с такой непосредственной очевидностью, как это может показаться на первый взгляд.

 

Даже если предпосылки в общих чертах сами по себе установлены и правильно, то даже и тогда в применении функционального метода легко может вкрасться ошибка недоучета некоторых функций, более мелкого масштаба, но тем не менее препятствующая правильному оформлению вещи.

 

Так, например, примитивно понимаемая функция стула состоит в создании предмета, на котором можно было бы сидеть, но только тщательное изучение всех привходящих этой функции обстоятельств, изучение того, для какой работы предназначен стул, для какого помещения и условий, из какого материала и т.д., — может дать окончательный и исчерпывающий материал для оформления этого стула. То же, конечно, остается в силе и по отношению к любому отдельному элементу архитектуры.

 

Далее в своем дальнейшем развитии, вопрос материализации определенной функции сейчас же выдвигает перед архитектором целый ряд проблем чисто архитектурного мастерства, т.-е. учета всех особенностей и возможностей употребляемого материала и учета всех возможностей психо-оптического воздействия.

 

Другими словами, материал должен не только удовлетворять своему прямому назначению, но и целому ряду привходящих обстоятельств, функционально раскрывая все свои естественные возможности цвета, фактуры, обработки и пр. Никогда еще все эти вопросы не играли такой большой роли, как именно теперь, и это, конечно, объясняется тем, что старая архитектура материалом лишь „подавала» форму, а следовательно само собой не в такой степени интересовалась качеством этого материала.

 

Если, например, дверная ручка какого-нибудь классического дома изображала коринфскую колонну или какую-нибудь из Венер, то, конечно, не так важно из какого материала она ее изображает — все равно настоящую мраморную колонну или живую Венеру вместо ручки не поставишь. Но когда дверная ручка — лишь функция своего назначения, то вопрос самого материала, его плотности, обработки, блеска, полировки и пр. — становится кардинальным вопросом данной частной архитектурной проблемы.

 

И, конечно, совершенно не случайно, что наиболее современные продукты новой культуры: авто, самолет, или какая-либо машина особенно поражает нас качеством употребляемых материалов, разнообразием своих фактур и поверхностей, всегда функционально оправданных. И, конечно, правильно понимаемый метод функционального мышления заставляет нас перенести на элементы архитектуры тоже сугубо внимательное изучение используемых материалов и их технической обработки, отныне становящееся одним из крупнейших вопросов материального оформления архитектуры.

 

Но точно так же чрезвычайно важной проблемой становится проблема правильного учета психо-физического воздействия элементов архитектуры. Форма должна не только выполнять свое основное назначение, но и выполнять его с максимальной ясностью и восприниматься нашим психо-физическим аппаратом с минимальной потерей энергии восприятия.

 

Вопросы окраски поверхности, например, становятся иногда не только вопросами, играющими только техническую роль, но и сложными вопросами нашей психо-гигиены. Современная психо-физиология отлично знает, что целому ряду функциональных назначений способствуют свои наиболее благоприятствующие цвета.

 

Точно также форма окна, его членение, его пропорции должны изменяться в зависимости от функционального назначения. Всем известно, как болезненно воспринимаются вашим глазом ошибки или нарушения какого-либо ритмического распорядка, если они не получают в нашем сознании какого-либо немедленного функционального оправдания.

 

И точно так же вопрос формы каких-либо пространственных величин есть сама по себе сложная архитектурная задача; функционально решить зал для каких-либо докладов, значит не только создать емкость для N-го количества слушателей, но и создать такую обстановку, в которой эти слушатели с максимальным удобством могли бы выполнить здесь свои функции, — при чем под удобством следует понимать не только внешне физические условия, но и сложную систему нашего психо-физического аппарата.

 

Таким образом следует со всей категоричностью установить, что метод функционального мышления ни в каком случае не уничтожает чрезвычайно важной задачи архитектурного оформления, он только устанавливает законы этого оформления, заставляя архитектора находить его в элементах функционально оправданных, перенося его из области отвлеченных эстетических прибавок и умозаключений к самой организации чисто архитектурной задачи, к формальному использованию всех утилитарных и конструктивных возможностей, всегда коренящихся во всяком архитектурном задании.

 

И точно так же четко устанавливается методом функционального мышления взаимоотношение между техникой и формой в передовой современной архитектуре. 

 

Уничтожая в корне дуалистическое толкование формы и конструкции, наш метод заставляет архитектора всегда овладевать элементами конструкции, разрешая при помощи их определенную пространственную задачу, вытекающую из производственно бытовых предпосылок.

 

Ценность метода функционального мышления именно и заключается в органической цельности мышления, в невозможности каких бы то ни было дуалистических толкованнй.

 

Правильно организованные элемента техники должны в такой же мере оформлять задание, как это последнее определять появление в каждом отдельном случае тех или иных элементов техники.

 

Таким образом в целом ряде отдельных случаев мы обладаем элементами архитектурного целого, которое одновременно является и элементами формы и элементом техники.

 

Это-то и есть, независимо от того, как бы их ни называть, элементы новой архитектуры, которые могут четко кристаллизоваться лишь в результате правильно понимаемого метода функционального мышления.

 

Конкретные пояснения нашей мысли мы можем видеть в настоящем номере СА, посвященном в значительной своей части 2 вопросам, в обычной толковании, чисто технического характера: вопросу плоской крыши и проблеме механически открываемых стандартных окон, выполняемых заводским способом.

 

Что же это такое: вопросы техники или формы? Конечно, и то и другое, а в нашем толковании ни то ни другое в отдельности, а единые вопросы архитектуры, так как, появившись в результате высоко развитой современной техники, они становятся в наше время лучшими элементами оформления.

 

М. Я. Гинзбург

---

 

 

 

Группа компаний «Стена» — спонсор рубрики «Архив» на портале Tehne. com. Поставка из Европы и производство всех видов декоративных отделочных материалов и фасадных систем, дизайн-проекты.

 

Зачем нужен функциональный анализ будущим специалистам по прикладной математике и информатике

Программист факультета информационных технологий и программирования Денис Антипов рассказал, зачем нужен функциональный анализ будущим специалистам по прикладной математике и информатике.

Если Вам учиться легко, то Вы либо очень способны, либо Вас ничему не учат.

Татьяна Толстая

Меня недавно попросили написать текст о том, зачем на факультете информационных технологий и программирования Университета ИТМО нужен такой предмет, как функциональный анализ (как говорят студенты, функан), так как этот вопрос возникает не только среди студентов, но даже преподавателей. Существует и противоположная точка зрения: один наш выдающийся выпускник сказал, что никогда не стеснялся того, что окончил наш вуз, так как в программу, когда он учился, входили такие предметы, как функан и теория функций комплексной переменной. Другой незаурядный выпускник сказал, что после изучения функана, он лучше понял матан (математический анализ).

Меня в первую очередь удивил сам факт того, что у студентов и преподавателей возникает вопрос необходимости этого предмета в учебной программе. Во-первых, для меня вопрос «зачем нужен функан на КТ» стоит в одном ряду с вопросом «зачем нужна математика в школе». Он кажется нелепым по той причине, что функциональный анализ является одним из базовых математических предметов, что пояснено ниже.

Вопрос студентов удивил меня также и тем, что он задается, несмотря на то, что в наше время у всех есть доступ в Интернет. Если погуглить, то легко найти обсуждение этой темы. Например, по запросу «Why learn functional analysis» сразу можно выйти на [1], где приведены примеры применения и причины необходимости функционального анализа в учебной программе по прикладной математике. Указанное обсуждение является далеко не единственным в сети на эту тему. Если же вопрос ставить не только про функциональный анализ, а более общий: зачем вообще нужна чистая математика в учебных программах для обучающихся прикладной математике, то опять по запросу «Why we learn pure math» можно найти обсуждение и этого вопроса, например, в [2].

Правда, для всего этого надо знать английский язык. А тот, кто его не знает или не хочет знать, может затеять дискуссию, зачем в институте учить иностранный язык, и такое можно устроить с любым предметом, который дается весьма непросто, например, с физвоспитанием.

Далее меня удивило то, что студенты в течение многих лет не задавали этот вопрос (у них, по крайней мере, «не поворачивался язык» говорить об этом), и только в последние годы они не стесняются его задавать, причем в такой, например, форме: «Если я собираюсь делать сайты, то зачем мне нужны функан и диффуры?» Возникает вопрос, а туда ли они поступили, и мне кажется, что с такой мотивацией они скоро из вуза исчезнут.

Меня удивило также и то, что люди не задали этот вопрос много лет преподающему функан Николаю Юрьевичу Додонову, который преподает его не только у нас, но и на матмехе СПбГУ, или хотя бы мне, так как многие знают, что я имею отношение к преподаванию математики на кафедре. Мы могли бы объяснить или хотя бы посоветовать посмотреть, например, книгу [3], которая хотя и была издана давно, но приведенные в ней примеры актуальны до сих пор.

Несмотря на это, я все-таки понимаю необходимость написания этого текста. При этом своей задачей ставлю именно сбор разобщенной информации в одном месте. Хорошо, что у меня под рукой есть много источников информации, и я могу просто цитировать людей, которые умнее меня, вместо того, чтобы формулировать какие-то мысли самому. Хотя ближе к концу я добавлю и некоторые свои рассуждения.

На самом деле вопрос необходимости функана куда более глубокий, чем кажется, и уходит корнями в философские вопросы о методах познания. Для начала вспомним, что в Новое время (в XVII веке) появились два основных направления в философии науки — эмпиризм и рационализм, которые во многом противопоставляли себя друг другу [4]. В основе классического рационализма, главные принципы которого были сформулированы Декартом [5], лежит идея возможности логического познания мира. Она берет свое начало еще из «Аналитик» Аристотеля [6]. Эмпиризм, основателем которого принято считать Бэкона [7], напротив, считает возможным только чувственное восприятие мира и ставит единственным критерием истинности эксперимент.

В наше время большинство ученых сходится в том, что ни экспериментальная, ни теоретическая наука не самодостаточны, а дополняют друг друга, и потому они обе необходимы для расширения человеческих знаний. Более подробное рассуждение на эту тему в области эволюционных вычислений можно найти в первой части [8].

Разумеется, стоит признать, что до сих пор даже среди ученых встречаются люди, не признающие чисто теоретические или чисто практические работы (первые встречаются чаще). В этом я убедился на недавней International Conference on Parallel Problem Solving from Nature (PPSN 2018), где потратил минут десять своего доклада на то, чтобы объяснить одному китайцу необходимость теории в области эволюционных вычислений. Однако десяти минут было недостаточно, чтобы изменить мнение убежденного эмпирика, так как, повторюсь, данные вопросы являются философскими.

Функциональный анализ, как это следует из его названия, является теоретической наукой, как и многие другие ветви математики, такие как топология, теория чисел, теория игр и другие. Однако, несмотря на то, что они все являются неприкладными по своей сути, каждая из них нашла применение при решении практических задач. Топология используется в анализе данных (TDA — Topological Data Analysis) [9], теория чисел — в криптографии [10], теория игр — в экономике [11]. Функциональному анализу также было найдено практическое применение. Самым ярким примером является его применение в квантовой механике [12]. Однако сегодня многие студенты нашей кафедры не считают нужным изучать квантовую механику (и, как ни грустно, физику в целом), поэтому более близкий пример для КТ-шников — применение функана для оценки погрешности вычислений численных методов при решении различных задач, в том числе нелинейных, что описано в [3]. Отмечу, что в этой книге содержится много ссылок на другие работы, посвященные практическому применению функционального анализа.

В случае если читателю недостаточно примеров применения функана, отмечу, что он широко используется в теории вероятностей для анализа стохастических процессов [13]. В своей работе я пользуюсь функаном именно в этом контексте. Например, в моей последней публикации с Бенжамином Доерром [14] знания функционального анализа очень помогли осознавать особенности анализируемого стохастического процесса и получить новые научные результаты, например, разработать оригинальный метод анализа эволюционных алгоритмов.

Приведу еще одну причину, почему стоит изучать функан. Известно, что большинство известных математических результатов было получено просто потому, что математикам это было интересно, а не потому, что они знали про какое-либо их практическое применение заранее, которое, тем не менее, было найдено позже (иногда сразу же, а иногда и через много десятилетий): «ищите и обрящете».

Здесь можно вновь привести примеры топологии, теории чисел и теории игр, так как сначала появились эти ветви математики, а только потом люди нашли им практическое применение. Однако наиболее интересным мне кажется пример Джорджа Буля.

Он одним из первых пришел к идее, что математик должен оперировать символами, представляющими некоторые объекты, а не самими объектами. Буль утверждал, что математика не должна привязываться к чему-то реальному и должна быть абстрактной. Это привело его к разработке матлогики и булевой алгебры в 1847 году [15]. И хотя Буль очень хотел, чтобы его алгебра была примером чистой, неприкладной математики, все мы знаем, что после развития вычислительной техники работы Буля стали настолько прикладными, что современный мир просто не мог бы без них обойтись.

Продолжатель дела Буля — Клод Элвуд Шеннон окончил MIT по специальности «электротехника и математика». Это позволило ему приложить теорию Буля к релейно-контактным схемам. Однако мне рассказывали о выдающемся математике, который долго расспрашивал, существенно ли, что диод проводит только в одну сторону.

Таким образом, одной математики тоже может быть недостаточно, и именно поэтому в направлении подготовки или специальности нашей «кафедры» и есть слово «прикладная». Но прикладная математика, а еще и информатика. Последнее слово еще больше усугубляет необходимость изучения математики, так как оно является переводом c английского термина Computer Science — компьютерная наука. Тот, кто этого не понимает или не хочет понимать и учить, как говорится, свободен … от обучения у нас.

Кстати, если это так, то для познания компьютерной науки очень неплохо начать ей заниматься уже в студенческие годы, так, во-первых, выдающийся российский хирург Н. И. Пирогов говорил: «Отделить учебное от научного нельзя. Но научное без учебного все-таки светит и греет, а учебное без научного — только блестит», а, во-вторых, без получения хотя бы каких-то научных результатов магистерскую выпускную работу у нас не защитить. И еще. Не путайте национальный исследовательский университет, куда вы поступили, с профессионально-техническим училищем, курсами или даже институтом повышения квалификации, а также богодельней…

Возвращаясь к функциональному анализу, заметим, что он так же, как и булева алгебра, развивался не столько с целью практического применения, сколько ради расширения математических знаний. Хоть он и берет свое начало примерно в одно время, что квантовая механика, после получения основных результатов функана в квантовой механике произошел значительный прорыв [12]. Оказалось, что самосопряженные операторы как нельзя лучше подходят для описания изменений в квантовой системе. Более того, понятие «спектр оператора» оказалось тесно связанным с физическим спектром. Применение функционального анализа для оценки погрешностей было предложено только после того, как вычислительная техника достаточно развилась — с конца 40-х годов XX века. Если же говорить про применение функана к стохастическим процессам, то оно началось с квантовой механики. Кроме того, с развитием вычислителей появилось множество вероятностных алгоритмов, для анализа которых также были необходимы средства из функционального анализа.

Таким образом, математику и, в частности, функциональный анализ стоит изучать не только ради собственного интереса, но и для практической пользы, которая может быть получена позже, а, может быть, и не получена…

Три выдающихся математика имели результаты и в области функционального анализа. Это им не помешало, а, возможно, помогло, получить выдающиеся практические результаты. Первый из них — Джон фон Нейман (он считается основоположником современного функционального анализа), создавший структуру ЭВМ, которая повсеместно применялась до последнего времени. Второй — Норберт Винер (в функане известна теорема Пэли-Винера-Шварца) — создатель кибернетики, а еще известны фильтры Винера, которые совершенствовались сначала Хопфом, а потом — почетным доктором Университета ИТМО Рудольфом Калманом. Третий — Андрей Колмогоров (известна книга Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа. МГУ, 2006). Полученные им результаты в разных областях математики нашли многообразные применения в теории информации, теории вероятностей и теории алгоритмов.
И, наконец, даже если вы не хотите иметь ничего общего с квантовой физикой, численными методами и вероятностями, вам все равно целесообразно изучать функциональный анализ. Доктор физ-мат. наук, профессор Юрий Шполянский, выпускник Университета ИТМО 2000 года, сказал, что функциональный анализ был самым сложным предметом из всей учебной программы на кафедре, и что, хотя он сам не применяет его на практике, этот предмет, по мнению Юрия, является очень полезным для мозга.

Я полностью согласен с этими словами: в IT-индустрии, безусловно, много направлений, не требующих от программистов знаний в области функционального анализа, однако как можно добиться существенных успехов в этой области без хорошо развитого математического мышления? Павел Дуров наверняка не знает функана, но зато его брат Николай изучал функан точно, так как учился и защитил в свое время PhD по чистой математике [16]. Именно такая комбинация предпринимательского и математического талантов помогла братьям подняться до нынешних высот.

Если у Вас есть таланты Гейтса или Джобса, то вы, как и они, можете не учить математику, но в их компании на работу вас без знания математики вряд ли возьмут. Кстати, одно из часовых (!) собеседований Ивана Белоногова, когда он поступал на работу в компанию OpenAI [17], было посвящено теории вероятностей и линейной алгебре, и он нормально прошел это испытание, как, впрочем, и все остальные.

Для развития математического мышления мало одного математического предмета в семестр (как это у нас происходит в гуманитарной области). Для этого учебная программа должна содержать целый комплекс различных фундаментальных дисциплин, включающий в себя не только анализ (математический и функциональный), но и теорию вероятностей, матстатистику, дифференциальные уравнения, теорию функций комплексной переменной, теорию чисел и ряд других. Только тогда выпускник факультета сможет считать себя человеком с высшим образованием, а не стоять в одном ряду с программистами-самоучками, которые выучили несколько языков программирования с помощью Google для того, чтобы «кодить», что многим нравится делать вне зависимости от того, как результаты их «творчества» будут использоваться компаниями, в которых они работают.

Надо признать, что в последнее время в связи с развитием технологий, растет объем и число предметов, которые следует преподавать студентам нашего направления (в том числе факультативно). Однако это не значит, что нужно уменьшать объем математических дисциплин в учебной программе, а надо повышать требования к студентам. К нам идут одни из самых талантливых школьников России в надежде получить лучшее образование, и вуз должен отвечать ожиданиям не только самих студентов, но и их родителей. Не все поступающие могут справиться с нагрузкой, которую предполагает трудное обучение, однако это не является поводом подстраивать программу под них. В стране существует множество других программ, на которых обучают программированию, но с более простыми учебными планами. Я говорю не только об Университете ИТМО: в стране 450 вузов, в которых готовят IT-специалистов, которые могут составить народное IT-ополчение, в то время как мы готовим спецназ.

Подведем итоги:

1. У функана есть множество практических применений [3, 12, 13].

2. Функан является сложным предметом, но это не причина не изучать его, хотя бы как предмет по выбору.

3. Функан, как и любая другая математическая дисциплина, может оказаться полезным в самых неожиданных областях.

4. Функан вносит неоценимый вклад в развитие математического мышления.

Я очень надеюсь, что данный текст поможет тем, кто учится на нашей кафедре, лучше понять, почему им нужен функан.
Текст написан мною при участии Анатолия Абрамовича Шалыто, который был также инициатором его написания. Мы благодарны коллегам за рецензирование текста.

P. S. Прочтя этот текст, Федор Царев спросил: «Есть краткий ответ на этот вопрос?». Шалыто ответил: «Специальность, по которой обучаются наши студенты называется „Прикладная, но математика“, а еще и „информатика“ (по-английски — Computer Science), а науки без математики не бывает. В Японии в настоящее время гуманитарные предметы не считают наукой, если там нет математики, программирования, моделирования и т. д. А математики, в свою очередь, не бывает без функана. Как сказал наш молодой fellowship Никита Алексеев: „Если человек не учил функан, то о чем с ним разговаривать?“ Пока вы молоды, надо глубоко учить математику, а параллельно с этим и после — все то, что предлагается здесь». Федя продолжил: «Вот это хороший ответ! Не ясно только, зачем весь остальной текст нужен)))».

Список литературы

[1] What is the main purpose of learning about different spaces, like Hilbert, Banach, etc?

[2] What is the «purpose» of pure mathematics?

[3] Коллатц Л. Функциональный анализ и вычислительная математика. Мир, М. 1969.

[4] Львов А.А. Курс лекций по дисциплине «История и философия науки». Лекция 5. Эксперимент и классическая наука Нового времени.

[5] Декарт Р. Рассуждение о методе, с приложениями: Диоптрика, Метеоры, Геометрия. Классики науки. Изд-во Академии наук СССР, 1953.

[6] Аристотель. Аналитики. Госполитиздат, Ленинград, 1952.

[7] Klein J., Bacon F. In The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University, 2016.

[8] Doerr B., Doerr C. Theory for non-theoreticians / Proceedings of the 2016 on Genetic and Evolutionary Computation Conference Companion (GECCO ’16 Companion), p. 463−482, NY, USA, 2016.

[9] Appliedtopology — source material for topological data analysis.

[10] Goodrich M., Tamassia R. Algorithm design: Foundations, analysis, and Internet examples. 2002.

[11] Neumann J. Theory of games and economic behavior. Princeton University Press, Princeton, 2007.

[12] Neumann J., Beyer R. Mathematical Foundations of Quantum Mechanics. Investigations in physics. Princeton University Press, 1996.

[13] Bobrowski A. Functional Analysis for Probability and Stochastic Processes: An Introduction. Cambridge University Press, 2005.

[14] Antipov D., Doerr B. Precise runtime analysis for plateaus. CoRR, abs/1806.1 331, 2018.

[15] Boole G. The Mathematical Analysis of Logic: Being an Essay Towards a Calculus of Deductive Reasoning. Cambridge Library Collection — Mathematics. Cambridge University Press, 2009.

[16] Nikolay Durov in nLab.

[17] OpenAI.

Функциональный метод решения уравнений с параметрами

Функциональный метод решения уравнений с параметрами

Краснова Г.Г.

Астраханский институт повышения квалификации и переподготовки, Россия, 414000, г. Астрахань, ул. Ульяновых, 4, (8512) 61-85-93, [email protected]

1 pp. (accepted)

Изучение многих физических процессов и геометрических закономерностей часто приводит к решению задач с параметрами.

Решение задач с параметрами вызывают большие затруднения у школьников. Это связано с тем, что решение таких задач требует не только знания свойств функций и уравнений, умения выполнять алгебраические преобразования, но также высокой логической культуры и хорошей техники исследования. Трудности при изучении данного вида уравнений связаны со следующими их особенностями:

– обилие формул и методов, используемых при решении уравнений данного вида;

– возможность решения одного и того же уравнения, содержащего параметр различными методами.

Поэтому встает вопрос о выборе наиболее рационального метода решения уравнения с параметром. Школьный курс математики предполагает обучение учащихся различным методам решения уравнений: аналитическому; графическому; функциональному; методу замены; методу изменения ролей переменных; методу перехода от общего к частному; методу свободных ассоциаций [1, с.61].

Остановимся подробнее на функциональном методе. Функциональный метод решения уравнений с параметрами является составной частью и естественным развитием функциональной линии обучения математике. Однако рассмотрение функционального метода в программе средней школы на базовом уровне носит эпизодический характер, при изучении отдельных тем. В то же время масштабы использования данного метода при решении уравнений впечатляют. Многие уравнения и неравенства, содержащие параметр, намного быстрее и проще решаются именно с использованием данного метода. Можно выделить свойства функций, наиболее часто используемые при решении таких задач. Во-первых, кусочная монотонность большинства алгебраических и элементарных трансцендентных функций, во-вторых, свойства четности и нечетности, периодичность функций, в-третьих, свойства ограниченности области определения или области значения функции. В отличие от графического метода, знание этих свойств функций позволяет находить точные корни уравнения, при этом не строя графики функций. Таким образом, использование свойств функций способствует рационализации решений уравнений с параметрами.

Литература

1. Мирошин, В.В. Решение задач с параметрами. Теория и практика / В.В.Мирошин. – М.: Издательство «Экзамен», 2009. – 286 с.

---

Функциональный научный подход, функционализм в науке: VIKENT.RU

Функциональный подход в науке по Брониславу Малиновскому

«Функционализм как метод так же стар, как и первые ростки интереса к чужим, а следовательно, по общему мнению, диким и варварским, культурам, — у кого бы такой интерес ни возникал: у греческого историка Геродота, у французского энциклопедиста Монтескье или у немецкого романтика Гердера.

Если мне и довелось внести какой-то скромный вклад, то состоит он в создании этикетки функционализма для уже существующего корпуса научных идей, методов и  интересов; но и в этом отношении, в своей статье я ссылаюсь на своих предшественников, число которых составляет двадцать семь человек. Таким образом, вероятно, я действовал как акушер и крёстный отец младшей из всего беспорядочного нагромождения антропологических школ и продолжил практиковать maieutike techne (акушерское искусство) в обучении самого молодого поколения исследователей в данной области, следуя заветам одного великого учителя, который любил описывать свое дело как искусство повивальной бабки. Был и ещё один великий учитель, давший функционализму его девиз «по плодам их узнаете их» (Матф., 7,16). […]

Я предполагаю, что весь полевой опыт, равно как и внимательное рассмотрение действительно значимых проявлений организованного поведения у человека, показывают справедливость следующих аксиом:

A. Культура по своей сути представляет собой инструментальный аппарат, посредством которого человек оказывается в положении, позволяющем ему лучше справляться со специфическими конкретными проблемами, встающими перед ним в ходе его взаимодействия со средой для удовлетворения своих потребностей.

Б. Она является такой системой участников, видов деятельности и отношений, где каждая часть существует как средство для достижения определённой цели.

B. Она является целостным образованием, разные элементы которого взаимозависимы.

Г. Составляющие культуру виды деятельности, отношения и участники организованы по принципу решения жизненно важных задач в институты — такие как семья, клан, локальная группа, племя и организованные группы для сотрудничества в хозяйственной области, для политической,  юридической и образовательной деятельности.

Д. С динамической точки зрения, то есть, принимая во внимание типы деятельности, культура может быть разложена на ряд аспектов — таких как образование, социальный контроль, экономика, системы познания, верований и морали, а также виды творческого и художественного выражения. В любом из своих конкретных проявлений культурный процесс всегда включает в себя людей, находящихся в определённых отношениях друг к другу, а это значит, что они определённым образом организованы, используют артефакты и коммуницируют друг с другом при помощи речи или иных символических средств. Артефакты, организованные группы и символика — три тесно связанные между собой измерения культурного процесса. Какова связь между ними?

Обратившись для начала к материальному аппарату культуры, мы можем сказать, что каждый артефакт является либо инструментом, либо предметом непосредственного использования, то есть принадлежит к классу предметов потребления. В любом случае контекст, в котором предмет встречается, а также его форма обусловлены его использованием. Функция и форма связаны. […]

Данный анализ позволит нам точнее определить понятие функции. Нам следует подойти к функции через понятие использования или понятие вещи и отношения.

Как мы можем видеть, во всех видах деятельности использование некоторого объекта в качестве части поведенческого акта, определённого с точки зрения техники, права и ритуала, даёт возможность удовлетворить некую потребность. Плоды и коренья собираются, ловится рыба, животные добываются на охоте, доится и забивается скотина — всё это служит пополнению кладовой человека. После чего эти продукты проходят обработку и приготовляются к подаче на стол. Все завершается трапезой — индивидуальной или совместной. Так потребность в питании управляет огромным разнообразием процессов. Ни для кого не станет откровением, если скажут, что движение человечества вперед зависит от сытости его брюха, что толпу можно ублажить хлебом и зрелищами, и что материалистический фактор удовлетворительного снабжения продовольствием — одна из детерминант человеческой истории и эволюции. Функционалист лишь добавит к этому, что мотивы, управляющие частями этого процесса и дробящиеся на страсть к огородничеству и охоте, меркантильный интерес к выгодному обмену или сбыту и стремление щедро одарить ближнего, должны подвергаться анализу с отсылкой к главному побуждению, к побуждению голода. Обобщающей функцией всех процессов, составляющих культурно организованное снабжение сообщества, является удовлетворение первичной биологической потребности в питании.

Если мы обратимся к другому виду деятельности, например к добыванию и поддержанию огня, мы опять же сможем привязать его к основным видам использования огня — для приготовления пищи, поддержания температуры окружающей среды, а также для выполнения некоторых технических процессов. Разнообразие религиозных и светских, юридических и технических отношений, строящихся вокруг огня, очага, священного пламени, — всё это мы можем связать с основными биологически важными функциями огня.

Или возьмём жилище человека. Это материальный объект, конструкция из брёвен или веток, шкур животных, снега или камней. Форма, технология сооружения жилища, его составные части и обстановка — все они связаны с использованием жилища, которое, в свою очередь, замыкается на организацию домовладения, семейной группы и людей, находящихся на её обеспечении и у неё в услужении. Здесь, опять же, изучая технологические фазы сооружения жилища и элементы его структуры, следует держать в голове обобщающую функцию целостного объекта».

Бронислав Малиновский, Функциональная теория / Научная теория культуры, М., «О.Г.И», 1999 г., с.139, 142-143 и 145-146.

Функциональный метод 3.0 — JTM FIT

Добро пожаловать в последний выпуск серии «Функциональные методы»! Мы продолжаем развивать первые две программы в TFM 3.0 и действительно предоставляем самую крутую программу из всех!

Как и другие программы TFM, я специально разработал эту программу, чтобы обеспечить потрясающие результаты при наращивании тела, а не разрушении его. Каждая неделя будет основываться на предыдущей с систематической прогрессирующей перегрузкой и правильным прогрессированием движений.Каждая тренировка будет включать в себя подробную разминку, основную тренировку и заминку, чтобы убедиться, что вы тренируетесь целенаправленно и целенаправленно.

Чем TFM 3.0 отличается от TFM 2.0?

• Повышенная интенсивность: В версиях 1.0 и 2.0 мы медленно увеличивали интенсивность, чтобы постепенно перегрузить тело, чтобы максимально безопасно нарастить силу и мускулы. Мы ПОДНИМАЕМ УРОВЕНЬ на в версии 3.0!

• НОВЫЕ суперсеты: In 3.0 мы вводим метаболический суперсет, чтобы максимально увеличить мышечный рост и увеличить чистую силу. Будьте готовы добиться серьезных успехов!

• НОВИНКА Цепи: В версии 3.0 мы вводим трехкомпонентные циклические тренировки для наращивания мышечной массы, повышения функциональной силы, улучшения физической формы и одновременного измельчения жировых отложений.

• Потенциал после активации: В терминах плача, PAP — это когда вы выполняете тяжелое силовое движение, сразу за которым следует взрывное движение. В версии 2.0 мы представили тяжелую атлетику.В версии 3.0 мы выходим на новый уровень с помощью PAP. Будьте готовы поднять свою силу и взрывоопасность на новый уровень!

• НОВЫЕ тренировки: В этой программе все новое. Разминки и заминки, основные финишеры, комплексы гирь и штанги, тренировки всего тела, тренировки на толкание / тяга верхней части тела, тренировки ног и кардио / основные тренировки подвижности.

СЕЙЧАС настало время по-настоящему внести долгосрочные изменения. Перестаньте тратить время на посещение тренажерного зала без установленного распорядка.TFM 3.0 проведет вас на каждом этапе пути к тому, чтобы стать самым разносторонним спортсменом из возможных. Если вы готовы по-настоящему изменить свой способ тренировок, бросить вызов себе в процессе и превратиться в чудовище на другом конце, тогда приступим к работе!

Функциональный метод 2.0 — JTM FIT

Добро пожаловать во вторую часть серии «Функциональные методы»! Если вы на этой странице, то я знаю, что вы человек, серьезно настроенный изменить свой распорядок и вывести свои тренировки на новый уровень.

Как и в случае с функциональным методом 1.0, я специально разработал эту программу для получения потрясающих результатов при наращивании тела, а не разрушении его. Каждая неделя будет основываться на предыдущей с систематической прогрессирующей перегрузкой и правильным прогрессированием движений. Каждая тренировка будет включать в себя подробную разминку, основную тренировку и заминку, чтобы убедиться, что вы тренируетесь целенаправленно и целенаправленно.

Чем TFM 2.0 отличается от TFM 1.0?

• Увеличенный рабочий объем: в 1.0 строим прочный фундамент. В версии 2.0 количество подходов увеличится, и общий объем тренировки увеличится, чтобы вывести вашу тренировку на новый уровень. Это касается всех тренировок.

• НОВЫЕ движения / Более продвинутые модели движений: Мы поднялись на ступеньку выше в 2.0 с новыми упражнениями и тренировками, а также более продвинутыми моделями движений, чтобы построить прочный фундамент, который мы заложили в 1.0

• Heavy поднятие тяжестей на силу: 1.0 состояло из диапазонов повторений, направленных на наращивание мышц и выносливость.Это, безусловно, продолжится и в версии 2.0, но мы также добавим более тяжелые упражнения в более низком диапазоне повторений, чтобы повысить чистую функциональную силу.

• Будет NEW разминок и заминок, NEW комплексов с гирями, NEW тренировок на толкание / тяга, NEW тренировок для ног и NEW кардио / кора / тренировок на подвижность!

• Также будет NEW финалистов тренировок, которые действительно испытают вас и доставят самую сильную помпу!

СЕЙЧАС настало время по-настоящему внести долгосрочные изменения.Перестаньте тратить время на посещение тренажерного зала без установленного распорядка. TFM 2.0 проведет вас на каждом этапе пути к тому, чтобы стать самым разносторонним атлетом. Если вы готовы по-настоящему изменить свой способ тренировок, бросить вызов себе в процессе и превратиться в чудовище на другом конце, тогда приступим к работе!

мет (…) — Вызов функционального метода

---

SAP NetWeaver AS ABAP, версия 752, © SAP AG, 2017 г. Все права защищены.

ABAP — Документация по ключевым словам → ABAP — Справочник → Вызов и выход из программных единиц → Вызов блоков обработки → Вызов процедур → Вызов методов → Вызов статических методов →

мет (. ..) — Вызов функционального метода

Синтаксис

… { static_meth ()
| static_meth (a)
| static_meth (p1 = a1 p2 = a2 …)
| static_meth ( [ ЭКСПОРТ p1 = a1 p2 = a2 … ]
[ ИМПОРТ p1 = a1 p2 = a2 … ]
[ ЗАМЕНА р1 = а1 р2 = а2… ] ) } …

Эффект

Функциональный вызов функциональный метод static_meth в подходящем позиция чтения для функций и выражений. Код возврата метода, объявленного с использованием ВОЗВРАЩЕНИЕ используется как операнд, и его полная типизация определяет тип данных операнда. Фактические параметры, привязанные к выходные параметры и параметры ввода / вывода обрабатываются так же, как в автономные вызовы методов.

Семантика синтаксиса, используемого при передаче параметров, такая же, как и при вызовах автономных методов. Вызовы функциональных методов отличаются от вызовов автономных методов следующим образом:

• Код возврата в вызовах функциональных методов не может быть назначен фактическому параметру явно с помощью RECEIVING.
• Встроенные объявления для фактических параметров невозможны.
• Исключения, не связанные с классами, нельзя обрабатывать с помощью EXCEPTIONS.
  

Если код возврата метода имеет структурированный тип данных, вызов функционального метода может, как и структура, быть указан перед селектор компонентов структуры — и используйте его для доступа к компоненту структуры.

Если функциональный метод имеет то же имя, что и встроенная функция, функциональный метод вызывается всегда.

Если возникает исключение, когда вызов функционального метода используется в качестве операнда, исключение не всегда может быть обработано, и вместо этого может возникнуть ошибка времени выполнения (в зависимости от положения операнда).

Примечания

• В вызовах функциональных методов исключения на основе классов, распространяемые из метода, могут обрабатываться как обычно в управляющей структуре TRY или распространяться дальше. В Однако исключения функционального метода, не связанные с классами, всегда вызывают ошибку времени выполнения.
• То же самое и с возобновляемыми исключения в вызовах функциональных методов, как и для всех других методов. Если обработка может быть успешно возобновлена, выполнение оператора, вызванного в методе, может быть завершено.
• Цепочка методов возможна в тех позициях операндов, где могут быть указаны функциональные методы.
• Вызов функционального метода, первый метод которого является методом экземпляра, может быть введен с использованием экземпляра оператор NEW или оператор приведения CAST.
• Вызов одного функционального метода может использоваться как вызов прогнозирующего метода и как реляционное выражение.
• Вызовы функциональных методов могут быть вложены любым способом, а это означает, что встроенные объявления фактических параметров могут приводить к запутанным результатам.По этой причине встроенные объявления не разрешены.
• В случае успеха каждый вызов метода устанавливает системное поле sy-subrc в 0, что означает, что все операторы с вызовами функциональных методов изменяют значение этого поля.

Пример

Функциональный вызов метода. В отличие от примера для при вызове автономных методов результату присваивается код возврата. Однако встроенные объявления, сделанные в этом примере, здесь невозможны.

ОПРЕДЕЛЕНИЕ КЛАССА c1.
ОБЩЕСТВЕННЫЙ РАЗДЕЛ.
МЕТОДЫ КЛАССА do_something ИМПОРТ p1 ТИП i
p2 ТИП i
ЭКСПОРТ p3 TYPE i
p4 ТИП i
ВОЗВРАЩАЕМАЯ СТОИМОСТЬ (r) ТИП i.
КОНЕЦ.

ВНЕДРЕНИЕ КЛАССА c1.
МЕТОД do_something.
…
КОНЕЦ.
КОНЕЦ.

ДАННЫЕ: a1 ТИП i,
a2 ТИП i.

НАЧАЛО ОТБОРА.
ДАННЫЕ (результат) =
c1 => do_something (ЭКСПОРТ p1 = 333
р2 = 444
ИМПОРТ p3 = a1
р4 = а2).

Пример

Функциональный метод Факториал в этом примере имеет факт кода возврата типа int8, используемый в правой части присваивания в выражении.

ОПРЕДЕЛЕНИЕ КЛАССА математики.
ОБЩЕСТВЕННЫЙ РАЗДЕЛ.
МЕТОДЫ факториал
ИМПОРТ n TYPE i
ВОЗВРАЩАЕМАЯ ЗНАЧЕНИЕ (факт) ТИП int8.
КОНЕЦ.

КЛАСС РЕАЛИЗАЦИИ математики.
МЕТОД факториал.
факт = COND int8 (КОГДА n <0 ТО 0
ИНАЧЕ УМЕНЬШИТЬ int8 (
INIT f = CONV int8 (1)
ДЛЯ i = 1 ДО тех пор, пока i> n
СЛЕДУЮЩИЙ f = f * i)).
КОНЕЦ.
КОНЕЦ.

НАЧАЛО ОТБОРА.

DATA (результат) = 100 + NEW math () -> factorial (4).

Пример

Функциональный метод get в этом примере имеет структурированный код возврата, к компоненту carrname которого осуществляется доступ.

КЛАСС НОСИТЕЛЕЙ ОПРЕДЕЛЕНИЕ.
ОБЩЕСТВЕННЫЙ РАЗДЕЛ.
СПОСОБЫ ПОЛУЧИТЬ
ИМПОРТ ТИПА CARRR-Carrid
ВОЗВРАЩАЕМАЯ ЗНАЧЕНИЕ (r) ТИП рубцов.
КОНЕЦ.

КЛАСС перевозчиков ВНЕДРЕНИЕ.
МЕТОД ПОЛУЧИТЬ.
ВЫБРАТЬ ОДИН *
ИЗ рубца
ГДЕ carrid = @carrid
ВТО @r.
КОНЕЦ.
КОНЕЦ.

НАЧАЛО ОТБОРА.

cl_demo_output => отображение (НОВЫЕ носители () -> get (‘LH’) -carrname).

«Функциональный метод сравнительного правоведения» Ральфа Майклса

Тип документа

Глава книги

Абстрактные

Функциональный метод стал одновременно мантрой и bete noire современного сравнительного права.Споры о функциональном методе являются фокусом почти всех дискуссий о сравнительном праве в целом, о центрах и периферии научных проектов и интересов, о мейнстриме и авангарде, об этноцентризме и ориентализме, о конвергенции и плюрализме. , о технократическом инструментализме и культурном сознании и т. д. Неудивительно, что этот функциональный метод является химерой и как теория, и как практика сравнительного правоведения. Фактически, «функциональный метод» — это тройное неправильное название: не существует одного («самого») функционального метода, но многие, не все так называемые методы вообще являются функциональными, а некоторые проекты, заявляющие о его соблюдении, даже не следуют никаким узнаваемым метод. В этой статье функциональный метод сначала помещается в исторический и междисциплинарный контекст, чтобы увидеть его связи и отличия от дискуссий о функционализме в других дисциплинах. Во-вторых, он пытается использовать метод функционализма в самом методе, чтобы определить, насколько он функциональный. Это делает необходимым поместить функционализм в более широкие рамки — не в рамках развития сравнительного права, а вместо этого в рамках взлетов и падений функционализма в других дисциплинах, особенно в социальных науках.В-третьих, сравнение с функционализмом в других дисциплинах позволяет нам увидеть, что особенного в функционализме в сравнительном праве, и почему то, что в других дисциплинах по праву считалось бы методологическими недостатками, на самом деле может быть плодотворным для сравнительного правоведения. Этот анализ приводит к удивительным результатам. Обычно предполагается, что сила функционального метода заключается в его акценте на сходствах, стремлении к оценке и унификации права. На самом деле функциональный метод подчеркивает различие, он не дает нам критериев оценки и дает весомые аргументы против унификации.Кроме того, обычно предполагается, что функциональный метод недостаточно учитывает культуру и является редукционистским. Однако функциональный метод не только требует от нас взглянуть на культуру, но и позволяет нам лучше, чем другие методы, формулировать общие законы без необходимости абстрагироваться от специфики. Проблема в том, что функциональный метод, как обычно описывается, сочетает в себе ряд различных концепций функции: эволюционную концепцию, структурную концепцию, концепцию эквивалентности.Связь между этими различными концепциями внутри метода неясна, поэтому его стремления нереалистичны. Если мы просто реконструируем метод на основе функциональной эквивалентности как наиболее надежного из трех концепций функции и подчеркнем интерпретативный, а не научный подход, мы поймем, что функциональный метод может делать меньше заявлений, но в то же время менее открыт для некоторой критики, высказанной против него. Короче говоря, функциональный метод — сильный инструмент для понимания, сравнения и критики различных законов, но слабый инструмент для оценки и унификации законов.Это помогает нам терпимо относиться к иностранным законам и критиковать их, но в меньшей степени помогает нам критиковать наши собственные.

Цитата

Ральф Майклс, Функциональный метод сравнительного правоведения Оксфордский справочник сравнительного правоведения 339-382 (2006)

СКАЧАТЬ

С 31 октября 2005 г.

МОНЕТЫ

Доступно по адресу: https: // scholarship.law.duke.edu/faculty_scholarship/1249

Курс функциональных методов Face Fit — 6 недель доступа

Мы много часов тренируем свое тело, но забываем о лице!

Приведите лицо в форму в удобном для вас темпе!

Эта основанная на фактах онлайн-программа состоит из четырех частей, которые познакомят вас с основными принципами Face Fit и дадут вам навыки для отслеживания вашего прогресса.

С подпиской у вас будет доступ ко всем материалам курса и обучающим видео на 6-недельный период .Все видео можно смотреть неограниченное время в течение периода подписки, что дает вам гибкость в соответствии с вашим личным расписанием.

Учебные материалы, сопровождающие программу, включают бесплатную рабочую книгу, которую можно загрузить во время курса и сохранить в качестве справочного материала после завершения курса.

По окончании программы вы узнаете, как распознавать правильные движения лица и как оптимизировать черты лица.

ЧАСТЬ 1. Почему мы так выглядим

Конечно, наша генетика влияет на то, как мы выглядим, но это только уводит нас далеко и не определяет нашу судьбу лица.

Мы намного больше, чем лицо, которое мы видим снаружи — у нас есть 6 слоев между кожей и нашим черепом внизу. Каждый слой играет определенную роль в том, как наше лицо формируется и стареет на протяжении всей жизни.

ЧАСТЬ 2- Как мы движемся

Правильное движение лица и рта определяет то, как выглядит наше лицо — если вы не двигаете им, вы его теряете!

Наше лицо формирует свою постоянную форму и поддерживает наш выбор здоровья и обстоятельства, а также то, как мы дышим и двигаемся лицом прямо с момента нашего рождения. Узнайте, как наш язык и нос являются двумя наиболее важными чертами нашего старения лица.

ЧАСТЬ 3- Возрастные изменения

Нравится нам это или нет, но каждый год приносит изменения во всем нашем теле. Наша кожа, мышцы и кости меняются ежегодно примерно с 25-30 лет, и наше лицо часто оказывается первым местом, где мы замечаем эти изменения.

Узнайте, как и почему это происходит, и как мы можем замедлить эффекты старения.

ЧАСТЬ 4 — 6 этапов функционального метода подгонки лица

Как следует из названия, это не просто набор упражнений.Он называется функциональным методом , потому что каждое действие и упражнение помогает гарантировать, что вы не просто выполняете точечные упражнения на отдельных участках лица, но вы учитесь правильно использовать все лицо и свое дыхание, жевание и глотание мышц. — убедитесь, что правильные мышцы используются для правильной работы.

Часть 4 проведет вас через 6 шагов к фитнесу для лица, включая более 25 различных мероприятий.

Не забудьте скачать буклет Face Fit Functional Method .

Мы поделились с вами этим уникальным функциональным методом Face Fit , чтобы вы могли Привести свое лицо в форму и извлечь пользу от изучения этих навыков на всю оставшуюся жизнь!

Функциональные методы плотности

: теория и приложения

https://doi.org/10.1016/S0081-1947(08)60313-6Получение прав и содержимого

Сводка издателя

В этой главе представлено исследование основ, достижений и ограничений методы функционала плотности.Поскольку эти методы берут начало в описании облака зарядов в атомах как вырожденного неоднородного электронного газа Томасом и Ферми, в этой главе представлен обзор статистической теории Томаса – Ферми. В этой главе также обсуждается расширение Дирака, включающее обмен. Поскольку обсуждаются основы теории функционала плотности при повышенных температурах, глава включает краткий обзор теории Томаса – Ферми при ненулевой температуре. После нескольких основных понятий современной теории функционала плотности обсуждаются теорема Хоэнберга – Кона и ее основные расширения.Эта теорема формально завершает первоначальную теорию Томаса – Ферми, показывая, что основное состояние многоэлектронной системы действительно является уникальным функционалом ее электронной плотности. В этой главе представлено формальное обсуждение расширений исходной теоремы Хоэнберга – Кона, включая (1) спиновые и релятивистские эффекты и (2) повышенные температуры. При рассмотрении вычислительных процедур в главе представлена ​​связь метода переходных состояний Слейтера с теорией функционала плотности возбужденных состояний.После обоснования одночастичных уравнений процедуры расчета имеют дело исключительно с приближениями локальной плотности; поэтому представлен краткий отчет о приблизительных способах преодоления приближения локальной плотности. Обсуждаются приложения теории функционала плотности к твердым телам, первая из которых касается некоторых проблем, которые подпадают под теорию линейного отклика.

Рекомендуемые статьиЦитирующие статьи (0)

Полный текст

Copyright © 1984 Academic Press, Inc.Опубликовано Elsevier B.V.Все права защищены.

Рекомендуемые статьи

Цитирующие статьи

Кинетический анализ детергентности гемоглобина методом функционала плотности вероятности

Abstract

В этом исследовании тесты стирки проводились с использованием образцов, полученных путем загрязнения тканей гемоглобином, а кинетический анализ проводился на основе метода функционала плотности вероятности, который выражает очищающую способность с использованием двух параметров σ _rl (относится к механизму очистки) и μ _rl (относится к уровню очищающей способности).Этот метод позволяет обрабатывать неопределенности, характерные для промывки белков, исходя из предположения, что адгезия почвы и моющая способность находятся в соответствии с нормальным распределением. Определенное количество раствора гемоглобина вымачивали в ткани, сушили и обрабатывали паром, а затем использовали в качестве образца для теста на очистку. Два параметра σ _rl и μ _rl были рассчитаны на основе моющей способности (%) через 5 минут, 10 минут, 15 минут и 20 минут стирки с учетом различных pH и температуры. уровни, а также различные уровни концентрации и температуры додецилсульфата натрия (SDS).Основываясь на результатах, значение σ _rl показало, что гемоглобин был удален под действием растворения. Кроме того, μ _rl увеличивалось в соответствии с увеличением pH, концентрации SDS и температуры. Относительно μ _rl , соотношение ΔX + ΔY = Δ (X + Y) наблюдалось в нескольких случаях, где ΔX представляет влияние pH или концентрации SDS. , ΔY — температурный эффект, а Δ (X + Y) — комбинированный эффект.Следовательно, может существовать аддитивная взаимосвязь между эффектами pH и температуры, а также концентрацией SDS и температурными эффектами.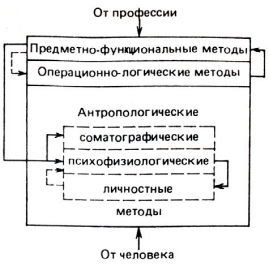

Образец цитирования: Оя М., Танигучи Ю., Фудзимура Н., Миямото К., Оя М. (2020) Кинетический анализ детергентности гемоглобина методом функционала плотности вероятности. PLoS ONE 15 (8): e0237255. https://doi.org/10.1371/journal.pone.0237255

Редактор: Анджани Кумар Тивари, Университет Бабасахеб Бхимрао Амбедкар (Центральный университет), ИНДИЯ

Поступило: 7 апреля 2020 г .; Одобрена: 22 июля 2020 г .; Опубликовано: 7 августа 2020 г.

Авторские права: © 2020 Oya et al.Это статья в открытом доступе, распространяемая в соответствии с условиями лицензии Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии указания автора и источника.

Доступность данных: Все соответствующие данные находятся в документе и его файлах с вспомогательной информацией.

Финансирование: Автор (Масару Оя) сообщил о получении следующей финансовой поддержки для исследования, авторства и / или публикации этой статьи: Эта работа была поддержана грантом на поддержку научных исследований (B) ( 17H01953) и грант на научные исследования (A) (17H00814) от Японского общества содействия науке (JSPS).

Конкурирующие интересы: Авторы заявили, что никаких конкурирующих интересов не существует.

Введение

В области медицины, с точки зрения гигиены, очистка пятен крови, приставших к медицинским устройствам и хирургическим материалам, имеет решающее значение. Поэтому по этому поводу были проведены серьезные исследования. Например, в нескольких исследованиях эффективность автоматической очистки сравнивалась с эффективностью ручной очистки медицинских инструментов, таких как специальные режущие инструменты, щипцы и эндоскопы [1–4].Кроме того, были проведены исследования влияния чистящих и дезинфицирующих средств на очистку медицинских устройств и материалов [5–7]. В нескольких исследованиях проводились тесты на аденозинтрифосфат (АТФ) и применялись альтернативные практические методы оценки моющих свойств [8–13], что подчеркивало важность мониторинга [14–16]. Было проведено несколько фундаментальных исследований, посвященных взаимодействию белков крови, таких как альбумин и гемоглобин, с поверхностно-активными веществами [17–19].

Кроме того, учитывая, что теоретический анализ явления очистки требует индекса мощности удаления грязи (т.е.е., очищающая способность), применение константы скорости уравнения первого порядка кинетики химической реакции привлекло значительное внимание исследователей [20–24]. Недавние кинетические исследования по удалению белка в основном были связаны с очисткой в ​​пищевой промышленности. Например, были исследования, которые включали оценку моющей способности сывороточного протеина по начальной константе скорости уравнения реакции первого порядка [25] и определение очищающей способности по начальному градиенту очистки желатина с использованием микровесов с кристаллами кварца. (QCM) [26].Кроме того, были представлены дискуссии о способности белков, прикрепленных к шарикам из нержавеющей стали, от начальной скорости десорбции [27], а влияние внешних электрических полей на удаление белков ферментами было разъяснено на основе оценки начальной скорости. [28]. Как упоминалось выше, во многих кинетических исследованиях, проводимых при отмывании белков, в качестве индекса использовался начальный градиент в приближении реакции первого порядка. Однако большинство практических данных по очистке трудно представить с помощью одного уравнения реакции первого порядка.

В общем, начальный наклон кривой удаления, зависящей от времени, имеет тенденцию быть больше, чем наклон теоретической кривой, а окончательный наклон имеет тенденцию быть меньше, чем теоретическая кривая. Поэтому было предложено предположение о процессе очистки во вторичной химической реакции [29] и метод анализа процесса очистки как суммы двух химических реакций первого порядка [30–32]. Однако трудно придать логический смысл механизму очистки с помощью таких методов, как скорость очистки, пропорциональная квадрату количества остаточного загрязнения, или разделение почвы на два типа.

Анализ с использованием простого уравнения реакции первого порядка затруднен тем, что при использовании одной и той же грязи легкость удаления зависит от состояния мест прикрепления и силы сцепления. Потенциальным методом смягчения этого изменения является использование функции плотности вероятности, которая является основой вероятностного анализа риска, который применялся во многих исследованиях; т.е. расчет вероятности обрушения конструкции [33] и оценка экологического риска химических веществ [34].

Была сделана попытка применить функцию плотности вероятности к оценке моющей способности. Результаты стирки масляного пятна красителя [35], грязи с частицами оксида железа [36] и имеющейся в продаже тестовой ткани для стирки, загрязненной смешанным пятном [37], были проанализированы в отношении двух параметров метода функционала плотности вероятности, среднего μ _rl и стандартное отклонение σ _rl распределения нагрузки удаления, предполагая, что очищающая способность следует нормальному распределению. Недавно было продемонстрировано, что один из двух параметров (σ _rl ) связан с типом почвы [38] и механизмом удаления почвы [39].

В этом исследовании тесты стирки проводились с использованием образцов, приготовленных путем загрязнения тканевых субстратов гемоглобином, который является одним из основных компонентов пятен крови; и влияние pH, температуры и концентрации поверхностно-активного вещества были исследованы на основе метода функционала плотности вероятности с акцентом на параметр μ _rl .Поскольку щелочной раствор часто используется в качестве моющего средства от белковых пятен, можно ожидать, что скорость стирки будет значительно меняться в зависимости от pH. Кроме того, поскольку SDS обладает гемолитическим действием, ожидается, что концентрация SDS в значительной степени способствует удалению пятен гемоглобина. Более того, поскольку и то, и другое можно рассматривать как разновидность химической реакции, можно предсказать, что на них влияет температура. Поэтому, чтобы подтвердить аддитивный эффект при различных условиях очистки, были исследованы правила суммирования между эффектами pH и температуры, а также между концентрацией поверхностно-активного вещества и температурными эффектами с использованием параметра μ _rl .

Материалы и методы

Подготовка материала

Для изготовления искусственно загрязненной ткани хлопчатобумажный тростник (Ассоциация прачечных в Японии) (плотность переплетения: основа 22,5 / 10 мм, уток 24,0 / 10 мм, вес: 15,2 мг / см. ² ) и гемоглобин (полученный из крови крупного рогатого скота. , Fujifilm Wako Chemicals) были использованы в качестве моделей белковых загрязнений. Гидроксид натрия (Fujifilm Wako Chemicals, гарантированный сорт) использовался для регулирования pH (температура контролировалась в стиральной машине) очищающей жидкости и додецилсульфата натрия (SDS, Fujifilm Wako Chemicals) в качестве поверхностно-активного вещества.

Примерно 250 г хлопчатобумажной ткани для тростника были погружены в 2 л 0,5% водного раствора карбоната натрия при 60–70 ° C. Затем ткань промывали дистиллированной водой, обезвоживали, сушили на воздухе и разрезали на секции размером 5 × 5 см ² . Почвенный раствор готовили растворением 2 г гемоглобина в 100 мл 0,1 н. Водного раствора аммиака и добавляли по каплям 400 мкл к каждому участку хлопчатобумажной ткани. Сразу после загрязнения была проведена сухая термообработка при 150 ° C в течение 2 минут в сушилке (DRD 320A, Toyo Engineering).После этого образцы обрабатывали паром в течение 8 минут в микроволновой печи (HEALSIO AX-2000, Sharp) с функцией генерации пара, а затем хранили в инкубаторе (BITEC-300, Shimadzu) при 20 ° C в течение 24 часов до тест на очистку.

Терготометр (Daiei Kagaku, TM-4) использовали для теста на очистку, и условия очистки были следующими. Пять образцов ткани для испытаний были промыты с использованием 1 л очищающего раствора при скорости перемешивания 80 об / мин, и время очистки составляло 5 мин на единицу. Моющая способность ( D %) была рассчитана на основе отражательной способности, измеренной с помощью цифрового колориметрического измерителя цветового различия (ZE-2000, Nippon Denshoku Industries Co. , ООО). Коэффициент отражения поверхности измеряли путем наложения пяти листов загрязненной ткани аналогичного цвета. Значение K / S было рассчитано с использованием уравнения Кубелки-Мунка (уравнение 1), при этом среднее значение, полученное путем измерения коэффициента отражения поверхности (значение Y) на передней и задней части образца, было значением R , и Скорость очистки рассчитывалась по формуле 2: (1) (2) где K — коэффициент поглощения света, S — коэффициент рассеивания света, D — эффективность очистки, K / S _S — значение K / S загрязненной ткани, K / S _W — значение K / S выстиранной ткани, а K / S ₀ — значение K / S необработанной белой ткани.Было обнаружено, что моющая способность K / S (%) загрязненной ткани, приготовленной с использованием этого метода, соответствует моющей способности (%), полученной с использованием метода Лоури после экстракции с использованием 0,1 н. Водного раствора NaOH, за исключением стирки с использованием отбеливания. агенты [40, 41].

Методология

В методе функционала плотности вероятности [35–39] предполагается, что сила сцепления почвы и сила удаления почвы находятся в соответствии с нормальным распределением, а эффективность очистки определяется на основе обоих распределений.Дальнейшие предположения заключаются в том, что сила сцепления почвы соответствует нормальному распределению со средним значением 0 и стандартным отклонением 1 (уравнение 3), а очищающая способность находится в соответствии с нормальным распределением со средним значением μ _rl и стандартное отклонение σ _rl (уравнение 4). (3) (4) где n — количество циклов очистки, x — случайная величина, а π — длина окружности.Чтобы вычислить величину снятия, вычисляется снимающая нагрузка φ (x) , полученная вычитанием кумулятивной функции г (x) из 1 (уравнение 5): (5) Расчет произведения φ (x) и распределения адгезии почвы дает количество удаленной грязи; которое может быть выражено уравнением 6, если n = 1, и уравнением 7, когда n > 1. (6) (7) Моющая способность (%) связана с изменением площади пика распределения силы сцепления. Отношение количества удаленного загрязнения ( R _n ) за счет циклов стирки n может быть рассчитано путем интегрирования f _Rn (x) (уравнение 8) и эффективность удаления ( D _n ) благодаря n циклам стирки может быть выражена уравнением 9.Следует отметить, что интегральное значение A ₀ (x) = 1. (8) (9) Более того, распределение остаточной грязи может быть получено путем вычитания распределения удаленных деталей из распределения перед очисткой. Когда n = 1 и n > 1, распределение может быть выражено уравнениями 10 и 11 соответственно.

(10) (11)

На основе этой теории, после определения σ _rl и μ _rl , распределение удаленной грязи и остаточной грязи может быть предсказано, а также количество удаляемой грязи и моющей способности (%) можно рассчитать. В этом исследовании среднее значение ( μ _rl ) и стандартное отклонение ( σ _rl ) распределения силы удаления были рассчитаны путем сравнения экспериментальной моющей способности (%) с расчетной моющей способностью ( %) относительно различных значений μ _rl и σ _rl . Затем с помощью метода наименьших квадратов были определены оптимальные значения μ _rl и σ _rl .Следует отметить, что диапазоны расчетов мк _rl и σ _rl составили –10,0–10,0 и 0,01–10,00 соответственно.

Соотношение между значениями μ _rl и σ _rl и зависимой от времени кривой скорости очистки показано на Рис.1 . При увеличении µ _rl кривая распределения моющей способности смещается вправо, а кривая моющей способности смещается вверх во всем диапазоне. Более того, с увеличением σ _rl ширина распределения очищающей способности увеличивается, а высота уменьшается. Кроме того, кривая скорости очистки показывает больший градиент на начальных стадиях и меньший градиент на конечных стадиях.

Результаты и обсуждение

Эффективность промывки при изменении pH и температуры

Зависимые от времени кривые моющей способности, полученные путем изменения pH с шагом 6, 9, 10 и 11 при температурах очистки 30 ° C, 40 ° C, 50 ° C и 60 ° C соответственно. в Рис 2 .Поскольку ожидалось, что эффективность очистки будет низкой, когда pH будет низким при низкой температуре, а эффект очистки из-за повышения температуры и pH будет трудно проявиться, минимальная температура была установлена ​​на 30 ° C. Во всех температурных условиях эффективность очистки непрерывно возрастала в соответствии с увеличением времени очистки, и было обнаружено, что моющая способность возрастает в соответствии с увеличением температуры и pH.

На основании анализа результатов теста на стирку по методу функции плотности вероятности, σ _rl в диапазоне 0.Было получено 39–0,70 ( табл. 1 ). Кроме того, была обнаружена прямая зависимость между σ _rl и механизмом очистки, причем механизм очистки изменялся в соответствии с увеличением σ _rl в следующем порядке: отделение твердого тела частицы почвы ( σ _rl : 0,01–0,6), растворение водорастворимых грунтов (ограничено веществами, которые обладают химической связывающей силой с волокном) ( σ _rl : 0.3–1.4), удаление маслянистой почвы водным раствором ПАВ солюбилизацией ( σ _rl : 1.0–2.0), эмульгирование маслянистой почвы водным раствором ПАВ и удаление дисперсией маслянистого вещества ( σ _rl : 3.0-) ( Рис. 3 ) [39]. Учитывая, что экспериментальное значение σ _rl находилось в диапазоне растворения водорастворимого грунта, предполагалось, что гемоглобин удаляется растворением.

Было обнаружено, что значение σ _rl незначительно увеличивается в соответствии с увеличением pH. Хотя пятна гемоглобина по существу удаляются растворением, механизм механического удаления твердых пятен более эффективен при низких уровнях pH, а чистое растворение более эффективно при высоких уровнях pH. Однако влияние вариации σ _rl было незначительным, учитывая, что не наблюдалось существенной разницы при вычислении μ _rl с константой σ _rl при среднее значение 5.2.

Размеры мкм _rl такие же, как и у распределения силы адгезии грязи. Кроме того, распределение силы адгезии грязи обычно соответствует логарифмическому графику, то есть шкале ln k , где k — общая константа скорости. График μ _rl относительно горизонтального масштаба 1/ T , который является обратной величиной абсолютной температуры, дал почти линейную зависимость ( Рис. 4 ).Следовательно, было обнаружено, что мк _rl может быть принято как важный термодинамический параметр.

Проверка правила суммирования значений pH и температуры

В этом исследовании увеличение pH и температуры привело к увеличению эффективности очистки в экспериментальных условиях. Выражая эффект увеличения pH как ΔD _(pH) , эффект повышения температуры как ΔD _(TMP) , а эффект увеличения pH и температуры как ΔD _{(pH + TMP)} , можно получить следующие соотношения:

1. Аддитивный эффект: D _{(pH + TMP)} = ΔD _(pH) + ΔD _(TMP)
2. Синергетический эффект: D _{(pH + TMP)} > ΔD _(pH) + ΔD _(TMP)
3. Эффект смещения: D _{(pH + TMP)} < ΔD _(pH) + ΔD _(TMP)

Таким образом, было исследовано установление аддитивного действия для девяти условий, при которых изменялись pH и температура, как показано в Fig. 5 .Моющая способность представлена ​​ μ _rl , а увеличение моющей способности представлено увеличением μ _rl . Например, если μ _rl при pH 7 выражается как μ _{rl (pH = 7)} и μ _rl при pH 10 выражается как μ _{мкл (pH = 10)} ; ΔD _(pH) , что является эффектом увеличения pH с 7 до 10, может быть выражено как μ _{rl (pH = 10)} — μ _{rl (pH = 7)} .Аналогично, в предположении, что μ _rl при температуре 30 ° C составляет μ _{rl (30 ° C)} и μ _rl при температуре 40 ° C составляет мкм _{rl (40 ° C)} ; ΔD _(TMP) , то есть увеличение очищающей способности при повышении температуры с 30 ° C до 40 ° C, может быть выражено как μ _{rl (40 ° C)} — мкм _{rl (30 ° C)} . Кроме того, ΔD _{(pH + TMP)} представляет собой увеличение μ _rl , когда температура и pH увеличиваются с 30 ° C до 40 ° C и с 7 до 10, соответственно. В этом исследовании был разработан новый метод определения аддитивного эффекта путем сравнения значений ΔD _{(pH + TMP)} и ΔD _(pH) + ΔD _(TMP) .

Рис 5.Определение аддитивного эффекта между повышением pH и повышением температуры при очистке гемоглобина: увеличение μ _rl из-за увеличения pH выражается как вертикальное значение, а увеличение μ _r из-за повышения температуры выражается горизонтальной величиной.

Кроме того, увеличение μ _rl из-за увеличения pH и температуры выражается диагональной стрелкой.Более того, аддитивность подтверждается, если рассчитанное значение (значение по вертикали + значение по горизонтали) значительно близко к соответствующему экспериментальному значению (значение красной диагональной стрелки).

https://doi.org/10.1371/journal.pone.0237255.g005

Существенные аддитивные эффекты наблюдались в условиях [pH 6, 40 ° C → pH 9, 50 ° C], [pH 9, 30 ° C → pH 10, 40 ° C], [pH 10, 30 ° C → pH 11, 40 ° C] и [pH 10, 40 ° C → pH 11, 50 ° C]. Кроме того, относительно значительные аддитивные эффекты наблюдались в условиях [pH 6, 50 ° C → pH 9, 60 ° C], [pH 9, 40 ° C → pH 10, 50 ° C] и [pH 10, 50 ° C → pH 11, 60 ° C].

Более того, в условиях [pH 6, 30 ° C → pH 9, 40 ° C] и [pH 9, 50 ° C → pH 10, 60 ° C] расчетные значения были значительно ниже измеренных значений. Эффективность очистки зависит от сложных факторов, таких как степень адгезии почвы и неравномерные условия очистки, что приводит к вариациям. Следовательно, трудно получить результаты теоретических расчетов с достаточной согласованностью. Однако следует отметить, что правило сложения было выполнено при семи из девяти условий.Кроме того, можно установить правило сложения между эффектом pH и влиянием температуры во время растворения гемоглобина в воде.

Влияние концентрации ПАВ и температуры

На рис. 6 представлена ​​зависящая от времени кривая эффективности очистки, когда концентрация SDS составляла 0 г / л, 1,5 г / л, 3,0 г / л и 5,0 г / л, а температура составляла 20 ° C, 35 ° C. C, 50 ° C и 65 ° C соответственно. Учитывая, что в этом эксперименте использовалась загрязненная ткань из предыдущего эксперимента, абсолютное значение моющей способности (%) нельзя сравнивать с таковыми из предыдущего эксперимента, как показано на рис. , рис. 2, .Моющая способность возрастает, когда концентрация поверхностно-активного вещества увеличивается на порядок 0 г / л → 0,15 г / л → 0,30 г / л; однако никаких значительных изменений между 0,30 г / л и 0,50 г / л не наблюдалось. Учитывая, что критическая мицеллярная концентрация (cmc) SDS, используемая в этом исследовании, составляла приблизительно 0,25 г / л, существенной разницы в способности удаления поверхностно-активного вещества не наблюдалось, когда она превышала cmc.

На основе метода функции плотности вероятности были получены результаты, представленные в Таблице 2 .Диапазон изменения температуры был больше, чем в эксперименте с pH (таблица 1), и σ _rl было значительно большим при 20 ° C. Это указывает на то, что растворение водой и эффект солюбилизации поверхностно-активным веществом были значительными при низких температурах. При температуре 35 ° C или выше σ _rl , по оценкам, немного увеличивалось в соответствии с увеличением концентрации поверхностно-активного вещества, и предполагалось, что поверхностно-активное вещество вносит вклад в действие растворения.В частности, в случае промывки с использованием воды, не содержащей SDS, в диапазоне температур 50–65 ° C, значение σ _rl указывает на то, что может быть реализован механизм удаления твердых частиц грязи. За исключением первоначально удаленных пятен, остальные пятна впоследствии было трудно удалить.

График μ _rl относительно 1/ T показан на Рис. 7 .Тесты очистки проводились в четыре этапа: 20 ° C, 35 ° C, 50 ° C и 65 ° C, и эффективность очистки при 65 ° C была немного ниже, чем указано на графике 1/ T . Это можно объяснить отсутствием повышения эффективности промывки при приближении к температуре денатурации белка.

Проверка правила добавления для влияния концентрации поверхностно-активного вещества и влияния температуры

Как правило, увеличение концентрации SDS и температуры приводит к увеличению скорости очистки.Таким образом, взаимодействие между эффектами увеличения концентрации SDS и температурой исследовали с использованием того же метода оценки, который применялся к эффекту влияния pH-температуры (рис. 8). Следовательно, расчетные и экспериментальные значения были относительно близки в условиях 20 ° C → 35 ° C и 35 ° C → 50 ° C

Рис. 8. Определение аддитивного правила между увеличением концентрации SDS и температурой при очистке гемоглобина: увеличение μ _rl из-за увеличения концентрации SDS выражается как вертикальное значение, и это связано с повышение температуры выражается горизонтальной величиной.

Увеличение μ _rl из-за увеличения концентрации SDS и температуры показано диагональной стрелкой. Более того, аддитивность подтверждается, если рассчитанное значение (значение по вертикали + значение по горизонтали) близко к соответствующему экспериментальному значению (значение красной диагональной стрелки).

https://doi.org/10.1371/journal.pone.0237255.g008

Более того, в каждом из трех случаев, когда концентрация SDS изменялась по отношению к изменению температуры с 50 ° C до 65 ° C, значительный Наблюдалась разница между расчетными и экспериментальными значениями.В условиях [концентрация SDS: 0 г / л → 1,5 г / л, 50 ° C → 65 ° C] и [концентрация SDS: 3,0 г / л → 5,0 г / л, 50 ° C → 65 ° C], экспериментальное значение было меньше расчетного. Ожидаемый эффект концентрации не был реализован, учитывая, что белок денатурировался, когда температура достигала 65 ° C.

И наоборот, в условиях [концентрация SDS: 1,5 → 3,0 г / л, 50 ° C → 65 ° C] экспериментальное значение было больше расчетного. Это область изменения концентрации как раз в сторону cmc, и в этом случае растворяющая способность SDS может иметь температурный эффект.В качестве альтернативы, диапазон температур мог находиться в пределах диапазона денатурации белка, что могло привести к вариациям экспериментальных значений.

Таким образом, трудно определить, выполняется ли правило добавления в диапазоне температур, в котором происходит денатурация белка. Однако в диапазоне 20–50 ° C наблюдалось аддитивное правило между эффектами концентрации SDS и температуры.

Выводы

На основе применения метода функциональной плотности вероятности к анализу моющей способности пятен гемоглобина, наблюдались аддитивные эффекты между эффектами pH и температуры, а также между концентрацией SDS и температурными эффектами при различных условиях. Более того, μ _rl было построено линейно по отношению к 1/ T в обоих случаях. Следовательно, μ _rl в этом исследовании можно использовать в качестве параметра со свойствами, аналогичными константе скорости. Общеизвестно, что белковые пятна денатурируются внешними раздражителями, такими как окисление и высокие температуры, что затрудняет их удаление. Однако использование метода функционала плотности вероятности, представленного в этом исследовании, привело к связи между скоростью очистки и механизмом очистки, что редко встречается в области очистки.В частности, был обнаружен его потенциал в качестве эффективного инструмента для оценки сложных эффектов. Считается, что в будущем, с точки зрения того, что протеазы ослабляют адгезию белковых пятен, могут быть проведены исследования для количественной оценки их влияния на эффективность очистки.

Список литературы

1. 1. Альфа М. Дж., Немес Р. Неадекватность ручной очистки для повторной обработки одноразовых трехпросветных сфинктертомов: тестирование моделирования использования, сравнивающее ручные методы с автоматическими методами очистки.Являюсь. J. Инфекционный контроль. 2003. 31: 193–207. https://doi.org/10.1067/mic.2003.22
2. 2. Альфа М.Дж., Немес Р., Олсон Н., Мулер А. Ручные методы субоптимальны по сравнению с автоматическими методами очистки одноразовых щипцов для биопсии, инфекционного контроля и больничной эпидемиологии. 2006; 27: 841–846. pmid: 16874645
3. 3. Альфа М.Дж., Олсон Н., ДеГань П. Автоматическая промывка с помощью системы обработки эндоскопов Reliance и ее эквивалент оптимальной ручной очистке, Am.J. Инфекционный контроль. 2006; 34: 561–570. https://doi.org/10.1016/j.ajic.2006.01.010
4. 4. Альфа М.Дж., Олсон Н., Мюррей Б.Л. Сравнение клинически значимых контрольных показателей и методов отбора проб каналов, используемых для оценки соответствия ручной чистке гибких желудочно-кишечных эндоскопов. Являюсь. J. Инфекционный контроль. 2014; 42: e1 – e5. Https://doi.org/10.1016/j.ajic.2013.08.007
5. 5. Penna TCV, Ferraz CAM. Очистка загрязненных кровью повторно обработанных ангиографических катетеров и спинномозговых игл, инфекционный контроль и больничная эпидемиология.2000; 21: 499–504. pmid: 10968714
6. 6. Голд КМ, Хитчинс ВМ. Оценка очистки дезинфицирующих салфеток на внешней поверхности медицинского изделия, загрязненной искусственной кровью или Streptococcus pneumonia, Am. J. Инфекционный контроль. 2013; 41: 901–907. https://doi.org/10.1016/j.ajic.2013.01.029
7. 7. Гонсалес Е.А., Нанди П., Лукас А.Д., Хитчинс В.М. Проектирование с учетом возможности очистки, Влияние материала, шероховатости поверхности и наличия загрязнений для анализа крови и бактерий на устройствах, Am.J. Инфекционный контроль. 2017; 45: 194–196. https://doi.org/10.1016/j.ajic.2016.07.025
8. 8. Альфа М.Дж., Фатима И., Олсон Н. Тест на аденозинтрифосфат — это быстрый и надежный инструмент аудита для оценки адекватности ручной очистки гибких каналов эндоскопа, Am. J. Инфекционный контроль. 2013; 41: 249–253. Https://doi.org/10.1016/j.ajic.2012.03.015
9. 9. Альфа М.Дж., Фатима И., Олсон Н. Валидация аденозинтрифосфата для аудита ручной очистки гибких каналов эндоскопа.Являюсь. J. Инфекционный контроль. 2013; 41: 245–248. https://doi.org/10.1016/j.ajic.2012.03.018
10. 10. Фусими Р., Такашина М., Йошикава Х., Кобаяши Х., Окубо Т., Наката С. и др. Сравнение аденозинтрифосфата, микробиологической нагрузки и остаточного белка как показателей для оценки чистоты гибких желудочно-кишечных эндоскопов. Являюсь. J. Инфекционный контроль. 2013; 41: 245–248. https://doi.org/10.1016/j.ajic.2012.02.030
11. 11. Smith GWG, McNeil J, et al.Оценка in vitro очищающей эффективности моющих средств, рекомендуемых для использования на стоматологических инструментах, Am. J. Инфекционный контроль. 2012; 40: e255–259. https://doi.org/10.1016/j.ajic.2012.05.009
12. 12. Альфа М.Дж., Олсон Н., ДеГанье П. , Симнер П.Дж. Разработка и проверка тест-полосок для быстрого использования для определения эффективности ручной очистки гибких каналов эндоскопа. Являюсь. J. Инфекционный контроль. 2012; 40: 860–865. https://doi.org/10.1016/j.ajic.2011.10.006
13. 13. Хамед ММА, Шамсея ММ, Алах ИДАНД, Саваф ГЕДЕ.Оценка средних значений бионагрузки на гибких желудочно-кишечных эндоскопах после клинического использования и очистки: Оценка эффективности процессов очистки. Александрийский медицинский журнал. 2015; 51: 95–103. https://doi.org/10.1016/j.ajme.2014.05.002
14. 14. Альфа М.Дж., Олсон Н., Фадхали А.А. Эффективность очистки моечных машин для медицинских устройств в медицинских учреждениях Северной Америки. J. Больничная инфекция. 2010. 74: 168–177. https://doi.org/10.1016/j.jhin.2009.06.030
15. 15.Альфа МДж. Мониторинг и повышение эффективности очистки медицинских и хирургических устройств, Am. J. Инфекционный контроль. 2013; 41: S56 – S59. https://doi. org/10.1016/j.ajic.2012.12.006
16. 16. Альфа М.Дж., Олсон Н. Физические и композиционные характеристики клинических выделений по сравнению с тестовыми почвами, использованными для проверки гибкости очистки эндоскопа. J. Больничная инфекция. 2016; 93: 83–88. https://doi.org/10.1016/j.jhin.2016.01.023
17. 17. Tardioli S, Bonincontro A, Mesa CL, Muzzalupo R.Взаимодействие бычьего сывороточного альбумина с сурфактантами Gemini. Журнал коллоидной и интерфейсной науки. 2010; 347: 96–101. pmid: 20362296
18. 18. Gelamo L, Silva CHTP, Imasato H, Tabak M. Взаимодействие бычьих (BSA) и человеческих (HSA) сывороточных альбуминов с ионными поверхностно-активными веществами: спектроскопия и моделирование, Biochimica et Biophysica Acta (BBA) — Структура белка и молекулярная энзимология. 2002; 1594: 84–99. https://doi.org/10.1016/s0167-4838(01)00287-4
19. 19. Лю В, Го Х, Го Р.Взаимодействие между гемоглобином и двумя поверхностно-активными веществами с разными зарядами. Международный журнал биологических макромолекул. 2007. 41: 548–557. pmid: 17889934
20. 20. Вон Т.Х., Виттон А. мл., Бэкон Л. Р., Свойства моющих растворов. Ind. Eng. Chem. 1941; 33: 1011–1019. https://doi.org/10.1021/ie50380a011
21. 21. Utermohlen WP Jr, Уоллес Э.Л., Исследования моющих средств. Текст. Res. J. 1947; 17: 670–688. https://doi.org/10.1177/004051754701701203
22. 22.Патрик Р.Л., Пейн О. мл. Скорость десорбции стеариновой кислоты с плоских поверхностей — новый метод. J. Colloid Sci. 1961; 16: 93–100. https://doi.org/10.1016/0095-8522(61)
    -1
    • 23. Дженнингс В.Г., Очистка циркуляции. III. Кинетика простой моющей системы. J. Dairy Sci. 1959; 42: 1763–1771. https://doi.org/10.3168/jds.S0022-0302(59)_-9
    • 24. Шотт Х. Кинетическое исследование моющей способности ткани. Варенье. Oil Chem. Soc. 1975. 52: 225–229.https://doi.org/10.1007/BF02639146
    • 25. Нагата А., Сакияма Т. , Ито Х, Тойомасу Т., Эномото Е., Нагаи Т. и др. Сравнительное исследование щелочной и ферментативной очистки поверхности нержавеющей стали, загрязненной β-лактоглобулином, бионаука, биотехнология и биохимия. 1995; 59: 2277–2281. https://doi.org/10.1271/bbb.59.2277
    • 26. Мюррей Б.С., Крос Л. Адсорбция β-лактоглобулина и β-казеина на металлических поверхностях и их удаление неионным поверхностно-активным веществом, что отслеживается с помощью микровесов на кристалле кварца.Коллоиды и поверхности B. 1998; 10: 227–241. https://doi.org/10.1016/S0927-7765(97)00066-0
    • 27. Сакияма Т., Тойомасу Т., Нагата А., Имамура К., Такахаши Т., Нагаи Т. и др. Эффективность протеазы в качестве чистящего средства для поверхностей из нержавеющей стали, загрязненных протеином, Journal of Fermentation and Bioengineering. 1998. 85: 297–301. https://doi.org/10.1016/S0922-338X(97)85678-4
    • 28. Htwe EE, Nakama Y, Yamamoto Y, Tanaka H, ​​Imanaka H, ​​Ishida N и др. Адсорбционные характеристики различных белков на поверхности металла при наличии внешнего электрического потенциала.Коллоиды и поверхности Б. 2017; 150: 118–124. https://doi.org/10.1016/j.colsurfb.2018.03.035
    • 29. Кисса Э. Кинетика механизмов моющего действия Часть I: Жидкие гидрофобные (маслянистые) почвы. Текст. Res. J. 1975. 4: 736–741. https://doi.org/10.1177/004051757504501007
    • 30. Борн М.С., Дженнингс РГ. Кинетические исследования моющей способности. I. Анализ кривых очистки. Варенье. Oil Chem. Soc. 1963; 40: 517–523. https://doi.org/10.1007/BF02822456
    • 31. Борн М.К., Дженнингс В.Г., Кинетические исследования моющей способности.II. Влияние возраста, температуры и времени очистки на скорость удаления почвы, J. Am. Oil Chem. Soc. 1963; 40: 523–530. https://doi.org/10.1007/BF02822457
    • 32. Борн М.С., Дженнингс РГ. Кинетические исследования моющей способности. III. Зависимость механизма Дюпре от поверхностного натяжения. Варенье. Oil Chem. Soc. 1965; 42: 546–548. https://doi.org/10.1007/BF02540100
    • 33. Фройденталь А.М., Гаррелтс Дж. М., Шинозука М. Анализ структурной безопасности. J. Struct. Div. (ASCE). 1966. 92: 267–325.https://cedb.asce.org/CEDBsearch/record.jsp?dockey=0014394
    • 34. Якобс Т.Л., Весилинд П.А. Вероятностный экологический риск опасных материалов. J. Envi. Англ. 1992; 118: 878–889. https://doi.org/10.1061/(ASCE)0733-9372(1992)118:6(878)
    • 35. Исикава Ю., Орито С., Оя М. Анализ эффективности стирки на основе концепции статистического распределения. J. Oleo Sci. 2006; 55: 511–519. Https://doi.org/10.5650/jos.55.511
    • 36. Исикава Ю., Орито С., Оя М.Статистический анализ эффективности мытья твердых частиц грязи. J. Oleo Sci. 2007. 56: 163–168. pmid: 17898478
    • 37. Исикава Ю., Оя М. Применение статистического анализа к смешанным моющим свойствам почвы. J. Oleo Sci. 2008. 57: 99–105. pmid: 18198466
    • 38. Фудзимото А., Оя М. Анализ процесса очистки нескольких видов почв методом функции плотности вероятности. J. Oleo Sci. 2017; 66: 1109–1120. pmid: 28924082
    • 39. Оя М. Связь между механизмом удаления загрязнений с тканей и параметром, полученным с помощью метода функционала плотности вероятности для анализа силы стирки.Текст. Res. J. 2019; 89: 2236–2246. https://doi.org/10.1177/00405175187
    • 40. Куроно Р., Нишио Н., Оя М. Получение количественной эффективности удаления белковых пятен из значения K / S для стирки тестовой ткани, загрязненной гемоглобином. J. Oleo Sci. 2013; 6: 223–229. https://doi.org/10.5650/jos.62.223
    • 41. Куроно Р., Оя М. Применимость улучшенной загрязненной гемоглобином ткани к тесту на отбеливание, J. Jpn Res. Доц. Текст. Конечное использование. 2013; 54: 750–757. https: // doi.org/10.11419/senshoshi.54.8_750

.