Расстояние между опорами лэп: Ничего не нашлось по запросу Proektsistem Rasstoyanie Mezhdu Oporami Lep %23I

07.03.202322.01.2023 alexxlab 0 Комментариев

Содержание

Одноцепная опора, двухцепная, угловая опора, концевая, ответвительная опора ЛЭП. Словарь

В вашем браузере отключен Javascript. Сайт может работать некорректно.

Главная
/
Словарь терминов

– система энергетического оборудования, предназначенного для передачи электрической энергии.

Воздушная линия (ВЛ)
– устройство для передачи электроэнергии по проводам, расположенным на открытом воздухе и прикрепленным с помощью изоляторов и арматуры к опорам.

Опора ЛЭП
– опора воздушной линии электропередачи – сооружение для удержания проводов и при наличии грозозащитных тросов воздушной линии электропередачи и оптоволоконных линий связи на заданном расстоянии от поверхности земли и друг от друга.
Каталог опор ЛЭП ГК ЭЛСИ

Опора одноцепная
– опора воздушной линии электропередачи, несущая одну трёхфазную линию (три электропровода).

Опора двухцепная
– опора воздушной линии электропередачи, несущая две трёхфазные линии (шесть электропроводов).

Анкерная опора
– опора воздушной линии электропередачи, воспринимающая усилия от разности тяжения проводов, направленных вдоль ВЛ.

Анкерный пролет
– это расстояние между двумя анкерными опорами ВЛ, на которых жестко закреплены провода.

Угловая опора
– опора воздушной линии электропередачи, рассчитанная на тяжение проводов с усилиями, действующими по биссектрисе внутреннего угла, образуемого проводами в смежных пролётах.
Угловая опора в каталоге опор ЛЭП ГК ЭЛСИ: ВЛ 10 кВ, ВЛ 35 кВ, ВЛ 110 кВ

Концевая опора
– опора воздушной линии электропередачи, которая воспринимает направленные вдоль линии усилия, создаваемые нормальным односторонним тяжением проводов; концевые опоры устанавливают в начале и конце ВЛ.

Концевая опора в каталоге опор ЛЭП ГК ЭЛСИ: ВЛ 10 кВ, ВЛ 35 кВ

Промежуточная опора
– опора воздушной линии электропередачи, служащая для поддержания проводов на определенной высоте от земли и не рассчитанная на усилия со стороны проводов в продольном направлении или под углом.

Ответвительная опора и перекрёстная опора
– опоры воздушных линий эпектропередачи, на которых выполняются ответвления от ВЛ и пересечения ВЛ двух направлений.

Провод
– элемент ВЛ, предназначенный для передачи электрического тока.

Грозозащитный трос
– элемент ВЛ, предназначенный для защиты проводов ВЛ от прямых ударов молнии. Трос заземляется или изолируется от тела опоры (земли) и, как правило, располагается над проводами фаз.

Тяжение провода (троса)
– усилие, направленное по оси провода (троса), с которым он натягивается и закрепляется на анкерных опорах ВЛ.

Габарит воздушной линии
– расстояние от низшей точки провисания провода до поверхности земли.

Стрела провеса провода (f)
– расстояние по вертикали между прямой линией, соединяющей точки подвеса провода, и низшей точкой его провисания.

Габаритная стрела провеса провода (fгаб)
– наибольшая стрела провеса провода в габаритном пролете.

Пролет ВЛ
– расстояние между соседними опорами воздушных линий электропередачи.

Габаритный пролет (lгаб)
– пролет, длина которого определяется нормированным вертикальным расстоянием от проводов до земли при установке опор на идеально ровной поверхности.

Весовой пролет (lвес)
– длина участка ВЛ, вес проводов (тросов) которого воспринимается опорой.

Ветровой пролет (lветр)
– длина участка ВЛ, с которого давление ветра на провода и грозозащитные тросы воспринимается опорой.

Вибрация проводов (тросов)
– периодические колебания провода (троса) в пролете с частотой от 3 до 150 Гц, происходящие в вертикальной плоскости при ветре и образующие стоячие волны с размахом (двойной амплитудой), которая может превышать диаметр провода (троса).

Пляска проводов (тросов)
– устойчивые периодические низкочастотные (0,2 – 2 Гц) колебания провода (троса) в пролете с односторонним или асимметричным отложением гололеда (мокрого снега, изморози, смеси), вызываемые ветром скоростью 3 – 25 м/с и образующие стоячие волны (иногда в сочетании с бегущими) с числом полуволн от одной до двадцати и амплитудой 0,3.

Гирлянда изоляторов
– устройство, состоящее из нескольких подвесных изоляторов и линейной арматуры, подвижно соединенных между собой.

Линейная арматура для ВЛ
– это, в частности, элементы крепления изоляторов, средства защиты, зажимы, спиральные вязки.

Нормальный режим ВЛ
– состояние ВЛ при неповрежденных проводах или тросах.

Аварийный режим ВЛ
– состояние ВЛ при оборванных проводах или тросах.

Монтажный режим ВЛ
– состояние ВЛ при монтаже опор, проводов или тросов.

Населенная местность
– земли городов в границах их перспективного развития на 10 лет, пригородные и зеленые зоны, курорты, земли поселков городского типа в пределах поселковой черты и сельских населенных пунктов в пределах черты этих пунктов.

Ненаселенная местность
– земли единого государственного фонда, за исключением населенной и труднодоступной местности; незастроенная местность, хотя бы и часто посещаемая людьми, доступная для транспорта и сельскохозяйственных машин, огороды, сады, местность с отдельными редко стоящими строениями и временными сооружениями.

Труднодоступная местность
– местность, не доступная для транспорта и сельскохозяйственных машин.

Подвесной изолятор
– изолятор, предназначенный для подвижного крепления токоведущих элементов к опорам воздушных линий электропередачи, несущим конструкциям и различным элементам инженерных сооружений.

Усиленное крепление провода с защитной оболочкой
– крепление провода на штыревом изоляторе или к гирлянде изоляторов, которое не допускает проскальзывания проводов при возникновении разности тяжений в смежных пролетах в нормальном и аварийном режимах ВЛЗ.

Штыревой изолятор
– изолятор, состоящий из изоляционный детали, закрепляемой на штыре или крюке опоры воздушной линии электропередачи.

Траверса

– конструкция, расположенная на опоре воздушной линии электропередачи, к которой крепят изоляторы для проводов и др. арматуру. Служит для создания требуемого изолирующего воздушного промежутка и поддержки проводов.

Трасса ВЛ
– положение оси ВЛ на земной поверхности.

Тросовое крепление
– устройство для прикрепления грозозащитных тросов к опоре ВЛ, если в состав тросового крепления входит один или несколько изоляторов, то оно называется изолированным.

Электрическая сеть
– совокупность воздушных и кабельных линий электропередач и подстанций, работающих на определенной территории.

404 Страница не найдена

История Мосэнерго
- Очерки
  - 1887-1917
  - 1917-1941
  - 1941-1945
  - 1945-2005
  - 2005-н.в.
- Мосэнерго: вчера и сегодня
- Знаменательные даты
- Награды
- Тематические подборки
Музей
- История создания
- Новое на сайте
- Экспозиции
  - Предметы экспозиции
  - Виртуальный тур, экспозиция 2007 года
- Архив
  - Опись
  - Фотоархив
    - 1887 – 1917
    - 1917 – 1941
    - 1941 – 1945
    - 1945 – 2005
    - 2005 год – н.
      в.
    - Электростанции
    - Тематические подборки
    - Фотовыставки
  - Видеоархив
  - Карты
  - Альбомы
  - Плакаты
- Печатные издания
  - Корпоративные СМИ
  - Технический архив
  - Печатная продукция
  - Библиотека музея
- Сотрудничество
  - Материалы наших читателей
Энергетика в лицах
- Выдающиеся личности
- Руководители
- Сотрудники
- Ветераны энергетики
- Участники Великой Отечественной войны
- Почетные энергетики
- Книга памяти
Фотоархив
Мосэнерго сегодня
Контакты

Расчет минимального расстояния двух проводников высоковольтной линии электропередачи

Всемирный инженерно-технический журнал Том 03 № 03 (2015 г. ), идентификатор статьи: 60491, 8 стр.
10.4236/wjet.2015.33C014

Расчет минимального расстояния двух проводников высоковольтной линии электропередачи0006

¹ Шанхайский институт проектирования электроэнергетики, ООО, Шанхай, Китай

² Институт экономических и технологических исследований Шанхайской электроэнергетической компании, Шанхай, Китай

Электронная почта: [email protected], 424510732 @qq.com

Поступила в редакцию 9 августа 2015 г.; принято 15 октября 2015 г.; опубликовано 22 октября 2015 г.

АННОТАЦИЯ

При проектировании высоковольтных линий электропередач неизбежно требуется изменение расположения проводов, причем на расстояние между проводами непосредственно влияет изменение расположения проводов. О расстоянии между проводами трудно судить опытным путем. Поэтому необходимо срочно разработать способ точного расчета минимального расстояния между проводами при изменении расположения между двумя проводами и определить, может ли минимальное расстояние соответствовать требованиям стандартов и правил или нет. Благодаря мышлению, основанному на уравнении баланса и методе расчета пространственной кривой, был получен более точный метод расчета двух проводов в различных условиях, минимальное расстояние было получено, а чувствительность минимального расстояния была проанализирована на основе метода .

Ключевые слова:

Воздушные линии электропередачи, расстояние между двумя линиями, уравнение баланса проводов, провисание проводов

1. Введение

изменить режимы расположения проводов и т. д., например, пролет линии 500 кВ на линии 220 кВ, входной портальный пролет ВЛ и т. д. При возникновении вышеперечисленных ситуаций неизбежно требуется проверка минимального расстояния между двумя проводами, чтобы определить, удовлетворяет ли оно требованиям правил [1]. Однако трудности проверки заключаются в том, что (1) ситуация пересечения, которую необходимо проверить, часто бывает очень сложной, и два проверяемых провода сталкиваются с такими ситуациями, как разные типы, разные коэффициенты безопасности и т. д. (2) Как создание, так и решение уравнения пространственной кривой сложны, и, полагаясь на простой расчет искусственного моделирования, нельзя получить точное решение. (3) Расстояние между проводами различно из-за разных провисов в разных условиях работы, поэтому трудно судить о рабочем состоянии для минимального расстояния и т. д. В нашей работе выполнено много расчетных исследований, касающихся расстояния между фазами проводов. страна. В Справочнике [2] трехмерная САПР используется для создания трехмерной модели межфазного интервала проводов вводного пролета и своего рода метода расчета межфазного интервала проводов с использованием интерактивного трехмерного Предложена САПР по теории косой параболы и трехмерного левого преобразования расчета. В [3] изучен метод расчета минимального межфазного расстояния проводов с учетом парусности и без учета парусности, а также проанализированы расчетные примеры соответствующих проектов. В соответствии с вышеуказанными трудностями и текущим состоянием, уравнение пространственной кривой [4]-[6] проводов было точно установлено, и минимальное расстояние между двумя проводами было рассчитано с использованием интегрально-дифференциального метода пространственной кривой и инструмента Matlab с учетом провес проволоки при различных условиях работы на основе уравнения баланса проволоки. Одновременно была проанализирована точность метода расчета, и была систематически рассчитана чувствительность минимального расстояния между двумя проводами при изменении перепада высот мачты, изменении коэффициента безопасности, изменении пролета и т. д., принимая энерго- спасательный провод (алюминиевый многожильный провод с сердечником из алюминиевого сплава) в качестве примера.

2. Метод расчета минимального пространственного расстояния между двумя проводами

2.1. Создание уравнения пространственной кривой проводов

Акцент при расчете минимального расстояния между двумя проводами в пространстве заключается в установлении расчетной модели пространственной кривой проводов. Прежде всего, трехмерная прямоугольная система координат устанавливается путем принятия центра башни в качестве исходной точки, направления выдвижения луча в качестве оси X, направления выдвижения башни вверх в качестве оси Z и направления выносной линии провода в качестве оси Y. ось, как показано на рис.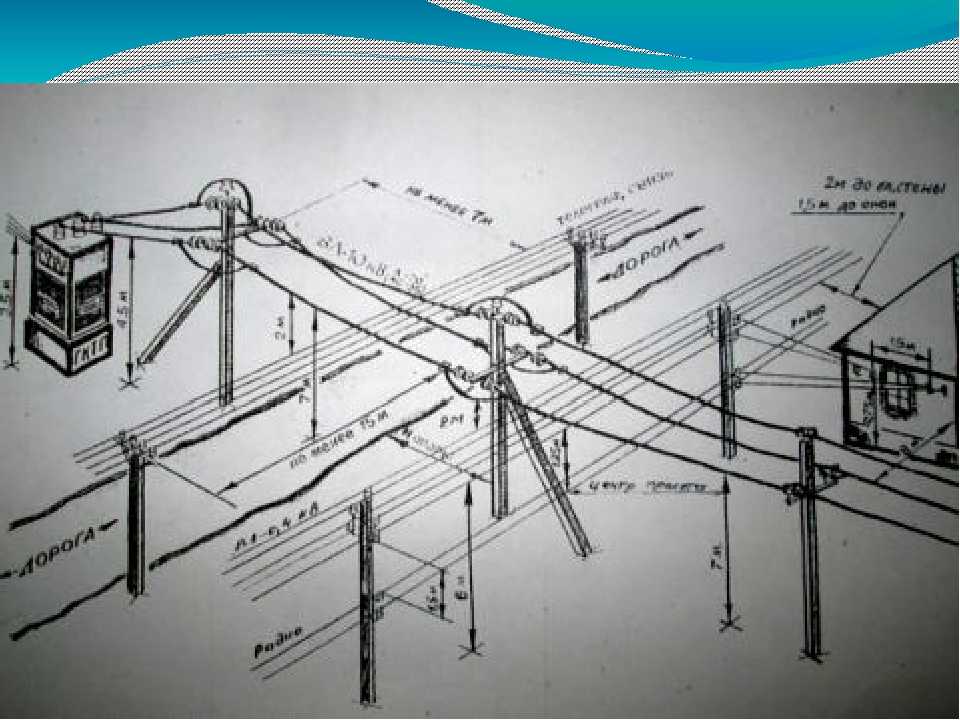 1.

Рис. 1. Примерная схема модельного расчета.

Уравнение пространственной кривой было получено на примере провода 1. Предполагается, что координаты точек подвеса в опоре провода Т ₁ и Т ₂ равны (x ₁ , y ₁ , z ₁ ) и (x ₂ , 6 y 3 _{, z ₂ ) соответственно, и тогда уравнение параметра пространственной кривой провода 1 между двумя точками подвеса выглядит следующим образом [5].}

где t — параметры пространственного положения.

Так же учитывался провес провода, и формула провеса наклонной параболы провода была согласно [4], тогда провес любой точки в пространстве провода равен

где f — провес провода с единицей м. γ — полная относительная нагрузка на проволоку в единицах Н/мм ² ・м. l — горизонтальное расстояние провода между двумя точками подвеса с единицей м. — расстояние от любой точки провода до точки подвеса (x ₁, у ₁, з ₁) с единицей измерения m. β — угол перепада высот с единицей. Затем в соответствии с моделью может быть определен метод расчета вышеуказанных различных параметров.

Расчетная упрощенная формула указанных выше параметров вводится в формулу провеса, затем

2.2. Корректировка пространственного уравнения провода с учетом парусности

У провода возникает определенная парусность под действием ветра, и угол его парусности равен и может быть получен. После намотки проволоки происходит изменение провиса по оси Z и изменение провиса в горизонтальной плоскости. Предполагается, что прямая, соединяющая точки подвеса проволоки и ось X в плоскости XY, образует угол, и тогда

, ,

Из-за того, что направление ветра по оси X не зафиксировано, когда направления ветра различны, переменная величина по осям X и Y линии между двумя точками подвешивания, вызванная провисанием провода, показана в таблице 1. с учетом синхронной парусности.

Следовательно, когда провод имеет намотку вдоль положительного направления оси X, пространственное уравнение провода может быть выражено как: получить

Таблица 1. Изменение осей X и Y, вызванное провисанием при различных направлениях ветра.

путем замены знака плюс-минус в приведенной выше формуле коррекции провисания.

2.3. Электрическое расстояние между двумя проводами в космосе

Уравнение параметров космического провода было получено с учетом провеса и ветра в соответствии с приведенным выше анализом. Предполагается, что два провода в пространстве — это линия1 и линия2, соответственно координаты точек подвеса линии1 равны A (x ₁ , y ₁ , z ₁ ) и B (x ₂ , y ₂ , z ₂ ) соответственно, а координаты точек подвеса линии 2 равны C (x 3 9006 y ₃ , z ₃ ) и D (x ₄ , y ₄ , z ₄ ) соответственно. Тогда расстояние между любыми точками двух проводов можно вычислить по формуле расстояния между двумя точками в пространстве.

Как видно, d ² — бинарное уравнение четвертой степени, а минимум d ² необходимо разрешить. Согласно дифференциальному методу пусть, а затем получается система бинарных кубических уравнений относительно функции положения t ₁ и t ₂. Впоследствии платформу Matlab можно использовать для решения d ² , таким образом получается минимум d. Бинарное кубическое уравнение имеет несколько наборов решений, поэтому необходимо определить диапазон значений функции. Более того, t ₁ и t ₂ появляются парами, d имеет единственное решение после определения значений функции, и его можно быстро решить в среде Matlab.

3. Анализ чувствительности минимума пространственной двухпроводности

При изменении режима расположения ВЛ необходимо проверить электрическое расстояние между проводами. В частности, обычно видно, что провод пролета входного портала преобразуется из горизонтального расположения портала в вертикальное расположение за пределами станции. Проанализировано, что чувствительность минимального расстояния между двумя проводами при изменении расстояния между оконечной башней и порталом, изменении перепада высот между оконечной башней и порталом, изменении коэффициента безопасности релаксационного пролета и т. д. в проектировании портальных пролетов линий 220 кВ и внедрении JL1/LHA1-465/210 (алюминиевая жила с сердечником из алюминиевого сплава).

3.1. Анализ модели

Модель анализа чувствительности показана на рисунке 2 [2].

Если тип провода JL1/LHA1-465/210, а параметры указаны в таблице 2.

3.2. Закон изменения минимального расстояния между двумя проводами при различных пролетах

1) Закон изменения расстояния с пролетом при различных условиях работы

Согласно положениям ГБ 50545-2010 минимальные расстояния между фазами в пролете под действием межфазных перенапряжение на 500 кВ и класс напряжения ниже 500 кВ приведены в таблице 3.

Регламент устанавливает только минимальное расстояние между фазами провода в условиях эксплуатации, а минимальное расстояние между фазами провода составляет 2,00 м при напряжении 220 кВ. Но минимальное расстояние между проводами не обязательно бывает в условиях эксплуатации. Следовательно, необходимо сравнить расстояние между проводами при высокой температуре и в рабочих условиях, как показано на рисунке 3.

Рисунок 2. Модель анализа чувствительности.

Таблица 2. Параметры энергосберегающего провода.

Таблица 3. Минимальные межфазные интервалы в пролете при действии межфазных рабочих перенапряжений.

Рисунок 3. Сравнение расстояний между проводами при различных условиях работы.

Как показано на рис. 3, минимальное расстояние между проводами в рабочих условиях явно больше, чем минимальное расстояние в условиях высокой температуры. Кроме того, когда минимальный пролет составляет 20 м, минимальные расстояния между фазами как в условиях эксплуатации, так и в условиях высоких температур могут соответствовать требованиям нормативных документов. Но минимальное расстояние проводов в условиях эксплуатации не может представлять другие условия для изучения минимального расстояния проводов. Следовательно, для изучения минимального расстояния между проводами, скорее всего, будет использоваться минимальное расстояние между проводами в условиях высокой температуры.

2) Закон изменения расстояния с пролетом при высокой температуре

В расчетной модели координаты двух точек подвеса провода 1 равны (7, 0, 27) и (3.5, y ₂ , 14) соответственно , а также координаты точек подвеса провода 2 равны (7.8, 0, 33.5) и (0, y ₄ , 14) соответственно. В дополнении

разница в расстоянии точек подвеса между проводом 1 и проводом 2 в терминальной башне составляет 6,5 м.

Рис. 4. Закон изменения минимального расстояния между двумя проводами при разных пролетах и разных коэффициентах безопасности.

Четко видно, что

(1) При одинаковом коэффициенте безопасности расстояние между двумя проводами в пространстве увеличивается с увеличением пролета. Однако амплитуда увеличения непрерывно уменьшается, а расстояние имеет тенденцию быть плавным и устойчивым. При k = 15 в качестве примера при пролете 20 — 30 м скорость изменения увеличения кратчайшего расстояния составляет около 5,5 %. При пролете в 110 — 120 м скорость изменения составляет всего 0,27%. А именно, чем больше пролет, тем слабее контроль минимального расстояния между двумя проводами в пространстве натяжением проводов.

(2) С увеличением коэффициента запаса становится все более очевидным закон изменения кратчайшего расстояния между двумя проводами в пространстве с пролетом, а также скорость изменения больше. При k = 3,4 скорость изменения пролета на 20 — 120 м составляет 3,8 %, а при k = 15 скорость изменения составляет 15,3 % при том же пролете. Поэтому при проектировании изменения способа расположения проводов совершенно необходимо проверить, соответствует ли требованиям расстояние между двумя проводами.

(3) При одинаковом пролете и разных коэффициентах безопасности наблюдается расслабление проводов и увеличение провеса проводов с увеличением коэффициентов безопасности. Благодаря этому минимальное расстояние между двумя проводами постоянно уменьшается.

(4) В регламенте требуется, чтобы межфазное расстояние проводов 220 кВ было не менее 2 м. Но только с учетом рабочего состояния в технике недостаточно, по-прежнему считается, что он соответствует требованию 2 м для расстояния между фазами при высокой температуре, более того, расстояние между фазами должно быть увеличено на 20% при допустимых условиях. При этом шаг фаз должен быть не менее 2,4 м. При расслаблении проводов необходимо одновременно контролировать коэффициент безопасности и пролет, например, при k = 15 пролет должен быть не менее 30 м, а при k = 20 пролет должен быть не менее 50 м.

3.3. Закон изменения минимального расстояния с пролетом при различной разнице высот

При проектировании входного/выходного козлового пролета часто приходится сталкиваться с тем, что разница между номинальной высотой оконечной башни и высотой козла больше. Следовательно, необходимо изучить изменение минимального расстояния двух проводов в пространстве при разной высоте. Так, при k = 15 изменение минимального расстояния в пространстве между двумя тросами входного козлового пролета необходимо первоначально учесть расчетом Δh = 13 м, 20 м, 30 м, 40 м и т. д.

Рис. 5. Закон изменения минимального расстояния между двумя проводами в пространстве с пролетом при различных перепадах высот.

Как видно, что:

(1) С увеличением разницы высот между терминальной башней и порталом минимальное расстояние между двумя проводами постоянно уменьшается, и чем больше разница высот, тем больше укороченная амплитуда является. Более того, когда Δh находится в пределах 13 м — 20 м, 20 м — 30 м и 30 м — 40 м, соответствующая скорость изменения составляет -0,80%, -1,50% и -1,9.4% соответственно при пролете 60 м.

(2) В пределах одного и того же пролета минимальное расстояние между двумя проводами постоянно сокращается с увеличением разницы высот. Однако по мере увеличения пролета кратчайшее расстояние между двумя проводами имеет тенденцию к постоянному изменению. А именно, чем больше пролет, тем слабее контроль кратчайшего расстояния между двумя проводами по разнице высот.

4. Выводы

На основе уравнения баланса проводов было точно установлено уравнение пространственных кривых проводов и рассчитано минимальное расстояние между двумя проводами в пространстве с использованием интегрально-дифференциального метода пространственной кривой и инструмента Matlab с учетом провисание проводов при различных условиях работы. Одновременно была систематически рассчитана чувствительность минимального расстояния между двумя проводами при изменении перепада высот башни, изменении коэффициента безопасности, изменении пролета и т. д., принимая энергосберегающий провод (алюминиевый проводник с сердечником из алюминиевого сплава) как пример. Кроме того, выводы получаются следующие.

(1) При одном и том же коэффициенте безопасности расстояние между двумя проводами в пространстве увеличивается с увеличением пролета, но амплитуда увеличения постепенно уменьшается, а расстояние остается стабильным. Причем, чем больше пролет, тем слабее контроль минимального расстояния между двумя проводами в пространстве за счет изменения натяжения провода, вызванного изменением коэффициента безопасности провода.

(2) При одном и том же пролете провисание троса увеличивается с увеличением коэффициента безопасности, что приводит к непрерывному уменьшению минимального расстояния между двумя тросами.

(3) С увеличением разницы высот мачты между обеими сторонами минимальное расстояние между двумя проводами постепенно уменьшается, и чем больше разница высот, тем больше укороченная амплитуда.

(4) В пределах одного и того же пролета минимальное расстояние между двумя проводами постепенно сокращается с увеличением разницы высот. Но чем больше пролет, тем слабее контроль кратчайшего расстояния между двумя проводами по разнице высот.

Процитировать эту статью

Wenjie Huang, Jinglin Zhu, Zhihang Du, Zheng Zhang, (2015) Расчет минимального расстояния двух проводников высоковольтной линии электропередачи. World Journal of Engineering and Technology , 03 , 89-96. doi: 10.4236/wjet.2015.33C014

Ссылки

1. GB 50545-2010. Нормы проектирования ВЛ 110кВ — 750кВ.

2. Yang, X.M., Feng, N. and Wu, S.P. (2012) Точная калибровка фазового расстояния диапазона приближения на основе трехмерной космической технологии. Электроэнергетическое строительство, 33, 46-48.

3. Бай, X.L., Ge, Q.L. и Ю, В.В. (2010) Анализ наименьшего фазового расстояния воздушной линии электропередачи. Электроэнергетика и инженерия, 26, 37-43.

4. Чжан, Д. С. (2003) Справочник по проектированию линии электропередачи. China Power Press, Пекин.

5. Гонг Ю.К., Лян Н.К., Гонг Ю.Г. (2009) Метод формулы для расчета электрического зазора проводника воздушной линии электропередачи. Электроэнергетическое строительство, 30, 24-27.

6. Рольфс А.Ф. и Шнайдер Х.М. (1983) Сила импульса переключения компактной линии электропередачи в плоской и треугольной конфигурациях. IEEE Transactions on Power Apparatus and Systems, 102, 822-831.

Открытый доступ SCIRP

Издательство научных исследований

Журналы от A до Z

Журналы по темам

Биомедицинские и биологические науки.
Бизнес и экономика
Химия и материаловедение.
Информатика. и общ.
Науки о Земле и окружающей среде.
Машиностроение
Медицина и здравоохранение
Физика и математика
Социальные науки. и гуманитарные науки

Журналы по тематике

Биомедицина и науки о жизни
Бизнес и экономика
Химия и материаловедение
Информатика и связь
Науки о Земле и окружающей среде
Машиностроение
Медицина и здравоохранение
Физика и математика
Социальные и гуманитарные науки

Публикация у нас

Представление статьи
Информация для авторов
Ресурсы для экспертной оценки
Открытые специальные выпуски
Заявление об открытом доступе
Часто задаваемые вопросы

Публикуйте у нас

Представление статьи
Информация для авторов
Ресурсы для экспертной оценки
Открытые специальные выпуски
Заявление об открытом доступе
Часто задаваемые вопросы

Подпишитесь на SCIRP

Свяжитесь с нами

	клиент@scirp. org
	+86 18163351462 (WhatsApp)
	1655362766

	Публикация бумаги WeChat

Недавно опубликованные статьи